题目内容
 如图,将直角梯形ABCD的一角沿对角线AC折叠,D点刚好落在∠ACB的平分线上,若梯形的一个底角为72°,则∠ACD的度数为
如图,将直角梯形ABCD的一角沿对角线AC折叠,D点刚好落在∠ACB的平分线上,若梯形的一个底角为72°,则∠ACD的度数为
- A.36°
- B.54°
- C.30°
- D.45°
A
分析:由折叠的性质可得,∠ACD=∠ACD',又CD'平分∠ACB,所以∠BCD'=∠ACD=∠ACD';又∠B=72°,根据两直线平行,同旁内角互补,可得∠BCD=108°-72°=108°,即可求得∠ACD的度数.
解答:∵AB∥CD,∠B=72°,
∴∠BCD=180°-∠B=180°-72°=108°,
∵CD'平分∠ACB,
∴∠BCD'=∠ACD',
∵∠ACD=∠ACD'(折叠的性质),
∴∠BCD'=∠ACD=∠ACD',
∴∠ACD=108°÷3=36°.
故选A.
点评:此题综合利用了折叠的性质、平行线的性质和角平分线的定义,难度中等.
分析:由折叠的性质可得,∠ACD=∠ACD',又CD'平分∠ACB,所以∠BCD'=∠ACD=∠ACD';又∠B=72°,根据两直线平行,同旁内角互补,可得∠BCD=108°-72°=108°,即可求得∠ACD的度数.
解答:∵AB∥CD,∠B=72°,
∴∠BCD=180°-∠B=180°-72°=108°,
∵CD'平分∠ACB,
∴∠BCD'=∠ACD',
∵∠ACD=∠ACD'(折叠的性质),
∴∠BCD'=∠ACD=∠ACD',
∴∠ACD=108°÷3=36°.
故选A.
点评:此题综合利用了折叠的性质、平行线的性质和角平分线的定义,难度中等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 以每秒1个单位长度的速度向点B移动,设移动时间为t秒.
以每秒1个单位长度的速度向点B移动,设移动时间为t秒. (2012•贵港)如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AD=5,BC=9,以A为中心将腰AB顺时针旋转90°至AE,连接DE,则△ADE的面积等于( )
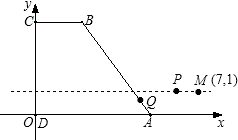
(2012•贵港)如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AD=5,BC=9,以A为中心将腰AB顺时针旋转90°至AE,连接DE,则△ADE的面积等于( )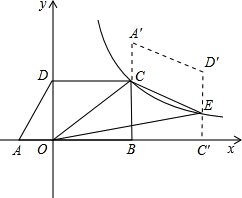 如图,在直角梯形ABCD中,AB∥CD,∠ABC=90°,将直角梯形ABCD放置在平面直角坐标系中.已知A(-2,0)、B(4,0)、D(0,3),反比例函数y=
如图,在直角梯形ABCD中,AB∥CD,∠ABC=90°,将直角梯形ABCD放置在平面直角坐标系中.已知A(-2,0)、B(4,0)、D(0,3),反比例函数y= 以每秒1个单位长度的速度向点B移动,设移动时间为t秒.
以每秒1个单位长度的速度向点B移动,设移动时间为t秒.