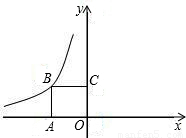
题目内容
(2008•呼和浩特)如图,已知二次函数图象的顶点坐标为C(1,1),直线y=kx+m的图象与该二次函数的图象交于A、B两点,其中A点坐标为( ,
, ),B点在y轴上,直线与x轴的交点为F,P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于E点.
),B点在y轴上,直线与x轴的交点为F,P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于E点.(1)求k,m的值及这个二次函数的解析式;
(2)设线段PE的长为h,点P的横坐标为x,求h与x之间的函数关系式,并写出自变量x的取值范围;
(3)D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在点P,使得以点P、E、D为顶点的三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.
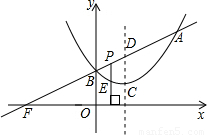
【答案】分析:(1)已知顶点C(1,1),设抛物线顶点式y=a(x-1)2+1,将A 代入可求抛物线解析式,从而可得B点坐标,已知A,B两点坐标,直线y=kx+m的图象经过A、B两点,代入可求k,m的值;
代入可求抛物线解析式,从而可得B点坐标,已知A,B两点坐标,直线y=kx+m的图象经过A、B两点,代入可求k,m的值;
(2)点P在直线y= x+2故P(x,
x+2故P(x, x+2),点E在抛物线y=x2-2x+2上,故E(x,x2-2x+2),∴h=PE=h=
x+2),点E在抛物线y=x2-2x+2上,故E(x,x2-2x+2),∴h=PE=h= x+2-(x-1)2-1.又P为线段AB上的一个动点(点P与A、B不重合),∴0<x<
x+2-(x-1)2-1.又P为线段AB上的一个动点(点P与A、B不重合),∴0<x< ;
;
(3)在P点运动过程中,∠DPE只可能是锐角或钝角,故直角顶点只有两种对应关系,即O对D,O对E,分两种情况,写成相似比,即△PDE∽△BOF,△PED∽△BOF,分别求解.
解答: 解:(1)设抛物线解析式为y=a(x-1)2+1
解:(1)设抛物线解析式为y=a(x-1)2+1
∵A 在抛物线上
在抛物线上
∴ =a(
=a( -1)2+1
-1)2+1
∴a=1
∴二次函数解析式为y=(x-1)2+1(或y=x2-2x+2)
令x=0得:y=2
即B(0,2)在y=kx+m上
∴m=2
把 代入y=kx+2
代入y=kx+2
得 ;
;
(2)h= x+2-(x-1)2-1
x+2-(x-1)2-1
=-x2+ x(0<x<
x(0<x< );
);
(3)假设存在点P,①当∠PED=∠BOF=90°时,由题意可得△PED∽△BOF
则
∴x= ,
,
∵0<x< ,
,
∴x= (舍去)
(舍去)
而x= <
<
∴存在点P,其坐标为
②当∠PDE=∠BOF=90°时,
过点E作EK垂直于抛物线的对称轴,垂足为K.
由题意可得:△PDE∽△EKD,△PDE∽△BOF
∴△EKD∽△BOF
则
∴ .
.
∵ ,
, 舍去
舍去
而 ,
,
∴存在点P,其坐标为
综上所述存在点P满足条件,其坐标为
 ,
, .
.
点评:本题考查了一次函数、二次函数解析式的求法,用坐标表示线段的长,及相似条件的探求,具有较强的综合性.
 代入可求抛物线解析式,从而可得B点坐标,已知A,B两点坐标,直线y=kx+m的图象经过A、B两点,代入可求k,m的值;
代入可求抛物线解析式,从而可得B点坐标,已知A,B两点坐标,直线y=kx+m的图象经过A、B两点,代入可求k,m的值;(2)点P在直线y=
 x+2故P(x,
x+2故P(x, x+2),点E在抛物线y=x2-2x+2上,故E(x,x2-2x+2),∴h=PE=h=
x+2),点E在抛物线y=x2-2x+2上,故E(x,x2-2x+2),∴h=PE=h= x+2-(x-1)2-1.又P为线段AB上的一个动点(点P与A、B不重合),∴0<x<
x+2-(x-1)2-1.又P为线段AB上的一个动点(点P与A、B不重合),∴0<x< ;
;(3)在P点运动过程中,∠DPE只可能是锐角或钝角,故直角顶点只有两种对应关系,即O对D,O对E,分两种情况,写成相似比,即△PDE∽△BOF,△PED∽△BOF,分别求解.
解答:
 解:(1)设抛物线解析式为y=a(x-1)2+1
解:(1)设抛物线解析式为y=a(x-1)2+1∵A
 在抛物线上
在抛物线上∴
 =a(
=a( -1)2+1
-1)2+1∴a=1
∴二次函数解析式为y=(x-1)2+1(或y=x2-2x+2)
令x=0得:y=2
即B(0,2)在y=kx+m上
∴m=2
把
 代入y=kx+2
代入y=kx+2得
 ;
;(2)h=
 x+2-(x-1)2-1
x+2-(x-1)2-1=-x2+
 x(0<x<
x(0<x< );
);(3)假设存在点P,①当∠PED=∠BOF=90°时,由题意可得△PED∽△BOF
则

∴x=
 ,
,∵0<x<
 ,
,∴x=
 (舍去)
(舍去)而x=
 <
<
∴存在点P,其坐标为

②当∠PDE=∠BOF=90°时,
过点E作EK垂直于抛物线的对称轴,垂足为K.
由题意可得:△PDE∽△EKD,△PDE∽△BOF
∴△EKD∽△BOF
则

∴
 .
.∵
 ,
, 舍去
舍去而
 ,
,∴存在点P,其坐标为

综上所述存在点P满足条件,其坐标为
 ,
, .
.点评:本题考查了一次函数、二次函数解析式的求法,用坐标表示线段的长,及相似条件的探求,具有较强的综合性.

练习册系列答案
相关题目
 ,
,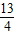 ),B点在y轴上,直线与x轴的交点为F,P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于E点.
),B点在y轴上,直线与x轴的交点为F,P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于E点.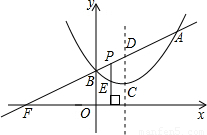
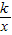 (k<0,x<0)的图象上,点P(m,n)是函数y=
(k<0,x<0)的图象上,点P(m,n)是函数y=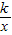 (k<0,x<0)的图象上异于B的任意一点,过点P分别作x轴、y轴的垂线,垂足分别为E,F.
(k<0,x<0)的图象上异于B的任意一点,过点P分别作x轴、y轴的垂线,垂足分别为E,F.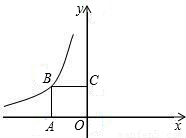
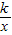 (k<0,x<0)的图象上,点P(m,n)是函数y=
(k<0,x<0)的图象上,点P(m,n)是函数y=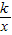 (k<0,x<0)的图象上异于B的任意一点,过点P分别作x轴、y轴的垂线,垂足分别为E,F.
(k<0,x<0)的图象上异于B的任意一点,过点P分别作x轴、y轴的垂线,垂足分别为E,F.