题目内容
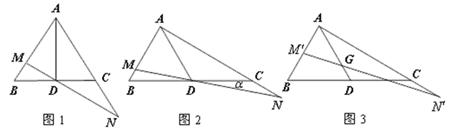
【题目】已知,AD是△ABC的中线,将BC边所在直线绕点D顺时针旋转![]() 角,交边AB于点M,交射线AC于点N,设AM=xAB,AN=yAC(x,y≠0).
角,交边AB于点M,交射线AC于点N,设AM=xAB,AN=yAC(x,y≠0).
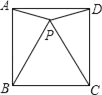
(1)如图1,当△![]() 为等边三角形且
为等边三角形且![]() °时,证明:△AMN∽△DMA;
°时,证明:△AMN∽△DMA;
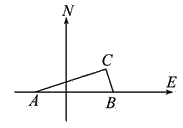
(2)如图2,证明: ![]() ;
;
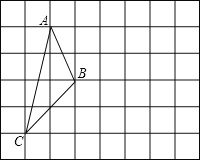
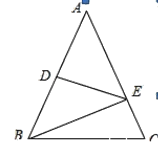
(3)如图3,当G是AD上任意一点时(点G不与A重合),过点G的直线交边AB于点![]() ,交射线AC于点
,交射线AC于点![]() ,设AG=nAD,
,设AG=nAD, ![]() ,猜想:
,猜想: ![]() 是否成立?并说明理由.
是否成立?并说明理由.
【答案】(1)证明见解析;(2)证明见解析;(3)猜想成立,理由见解析.
【解析】试题分析:(1)利用“两角法”证得两个三角形相似;
(2)如图1,过点C作CF∥AB交MN于点F,构建相似三角形:△CFN∽△AMN,利用该相似三角形的对应边成比例求得![]() .通过证△CFD≌△BMD得到BM=CF,利用比例的性质和相关线段的代入得到
.通过证△CFD≌△BMD得到BM=CF,利用比例的性质和相关线段的代入得到![]() ,即
,即![]() ;
;
(3)猜想: ![]() +
+![]() =
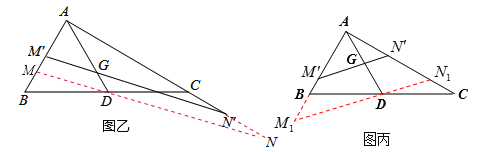
=![]() 成立.需要分类讨论:①如图乙,过D作MN∥M'N'交AB于M,交AC的延长线于N.由平行线截线段成比例得到
成立.需要分类讨论:①如图乙,过D作MN∥M'N'交AB于M,交AC的延长线于N.由平行线截线段成比例得到![]() ,易求
,易求![]() ,利用(2)的结果可以求得
,利用(2)的结果可以求得![]() ;
;
②如图丙,当过点D作M1N1∥M'N'交AB的延长线于M1,交AC1于N1,则同理可得![]() .
.
试题解析:解:(1)证明:如图1.在△AMD中,∵AD是△ABC的中线,△ABC为等边三角形,∴AD⊥BC,∠MAD=30°.又∵α=∠BDM=30°,∴∠MDA=60°,∴∠AMD=90°.在△AMN中,∠AMN=90°,∠MAN=60°,∴∠AMN=∠DMA=90°,∠MAN=∠MDA,∴△AMN∽△DMA;
(2)证明:如图甲,过点C作CF∥AB交MN于点F,则△CFN∽△AMN,∴![]() .
.
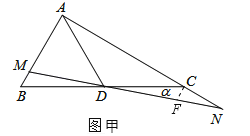
∵CF∥BM,∴∠B=∠DCF.在△CFD和△BMD中, 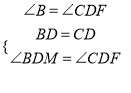 ,∴△CFD≌△BMD,∴BM=CF,∴
,∴△CFD≌△BMD,∴BM=CF,∴![]() ,∴
,∴![]() ,即
,即![]() ;
;
(3)猜想: ![]() +
+![]() =
=![]() 成立.理由如下:
成立.理由如下:
①如图乙,过D作MN∥M'N'交AB于M,交AC的延长线于N,则![]() ,∴
,∴![]() ,即
,即![]() ,由(2)知
,由(2)知![]() ,∴
,∴![]() ;
;
②如图丙,当过点D作M1N1∥M'N'交AB的延长线于M1,交AC1于N1,则同理可得![]() .
.

 名校课堂系列答案
名校课堂系列答案