题目内容
正方形ABCD的边长为4,P为CD边的延长线上一点,且PD=3,把△PAD绕顶点A旋转,使得点P落在直线BC上Q点,此时QC的长为________.
1或7
分析:分两种情况进行讨论,如图1,Q在BC之间,根据翻折变换性质,可知BQ=3,即CQ可求出,如图2,当Q点在CB的延长线上,利用勾股定理求出QB的长,进而求出QC的长度.
解答: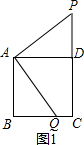 解:如图1,
解:如图1,
∵△ABQ是△ADP旋转得到的,
∴BQ=PD=3,
∵AD=BC=4,
∴CQ=1,
如图2,在Rt△ADP中,
∵AD=4,DP=3,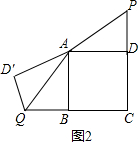
∴AP=5,
∵△AD′Q是△ADP旋转得到的,
∴AQ=5,
∵QB2=AQ2-AB2,
∴QB=3,
∴QC=QB+BC=7,
故答案为1或7.
点评:本题主要考查旋转的性质以及正方形的性质的知识点,解答本题的关键是进行分类讨论,此题难度不大.
分析:分两种情况进行讨论,如图1,Q在BC之间,根据翻折变换性质,可知BQ=3,即CQ可求出,如图2,当Q点在CB的延长线上,利用勾股定理求出QB的长,进而求出QC的长度.
解答:
 解:如图1,
解:如图1,∵△ABQ是△ADP旋转得到的,
∴BQ=PD=3,
∵AD=BC=4,
∴CQ=1,
如图2,在Rt△ADP中,
∵AD=4,DP=3,

∴AP=5,
∵△AD′Q是△ADP旋转得到的,
∴AQ=5,
∵QB2=AQ2-AB2,
∴QB=3,
∴QC=QB+BC=7,
故答案为1或7.
点评:本题主要考查旋转的性质以及正方形的性质的知识点,解答本题的关键是进行分类讨论,此题难度不大.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 附加题
附加题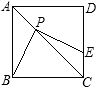 如图,正方形ABCD的边长为4,P为对角线AC上一点,且CP=3
如图,正方形ABCD的边长为4,P为对角线AC上一点,且CP=3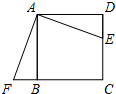 如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为
如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为 如图,正方形ABCD的边长为6,点M在边DC上,M,N两点关于对角线AC对称,若DM=2,则tan∠ADN=
如图,正方形ABCD的边长为6,点M在边DC上,M,N两点关于对角线AC对称,若DM=2,则tan∠ADN=