题目内容
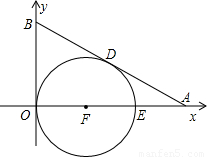
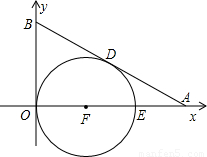
Rt△AOB中直角边OA、OB分别在x轴、y轴的正半轴上,O为坐标原点,以F为圆心的 圆与y轴、直线AB分别相切于O、D(如图),若AD=2,AE=1.
圆与y轴、直线AB分别相切于O、D(如图),若AD=2,AE=1.(1)求BD的长度;
(2)求经过A、B两点的直线的解析式;
(3)求经过E、D、O三点的二次函数的解析式;
(4)判断(3)中抛物线的顶点是否在直线AB上.
分析:(1)根据圆的切线的性质,连接DF,可得直角三角形,借助于方程,利用勾股定理求得圆的半径,利用相似求得BD的长;
(2)根据(1)的结论可得A,B的坐标,利用待定系数法可求得经过A、B两点的直线的解析式;
(3)首先求得点D的坐标,将点O,E,D的坐标代入二次函数的一般式,解方程组即可;
(4)求得抛物线的顶点坐标,再代入解析式,看是否左右相等即可.
(2)根据(1)的结论可得A,B的坐标,利用待定系数法可求得经过A、B两点的直线的解析式;
(3)首先求得点D的坐标,将点O,E,D的坐标代入二次函数的一般式,解方程组即可;
(4)求得抛物线的顶点坐标,再代入解析式,看是否左右相等即可.
解答: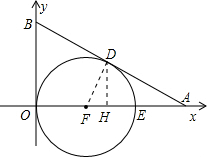 解:(1)设⊙F的半径为r
解:(1)设⊙F的半径为r
连接DF,∴BA⊥DF
∵AD切⊙F于D点
∴AD2=AE•AO即22=1•(2r+1)
∴r=
又Rt△ADF∽Rt△AOB
∴
=
即
=
∴AB=5,故BD=3;
(2)显然A(4,0)、B(0,3)
故设解析式为y=kx+3
将(4,0)代入得AB解析式y=-
x+3;
(3)过D作DH⊥AO于H,
∴DH=BO
∵△ABO∽△ADH
∴DH=
又∵DH∥BO
∴
=
,即
=
∴OH=
∴D点坐标为(
,
)
E点坐标(3,0)
设经过EDO的函数解析式为y=ax2+bx+c.
得
∴所求函数解析式为y=-
+
;
(4)(3)中的顶点为(
,
).
当x=
时,代入y=-
x+3=-
×
+3=
≠
故(3)的顶点不在直线AB上.
 解:(1)设⊙F的半径为r
解:(1)设⊙F的半径为r连接DF,∴BA⊥DF
∵AD切⊙F于D点
∴AD2=AE•AO即22=1•(2r+1)
∴r=
| 3 |
| 2 |
∴
| AD |
| AO |
| AF |
| AB |
即
| 2 |
| 1+3 |
1+
| ||
| AB |
∴AB=5,故BD=3;
(2)显然A(4,0)、B(0,3)
故设解析式为y=kx+3
将(4,0)代入得AB解析式y=-
| 3 |
| 4 |
(3)过D作DH⊥AO于H,
∴DH=BO
∵△ABO∽△ADH
∴DH=
| 6 |
| 5 |
又∵DH∥BO
∴
| BD |
| AB |
| OH |
| AO |
| 2 |
| 5 |
| OH |
| 4 |
∴OH=
| 8 |
| 5 |
∴D点坐标为(
| 8 |
| 5 |
| 6 |
| 5 |
E点坐标(3,0)
设经过EDO的函数解析式为y=ax2+bx+c.
|
得
|
∴所求函数解析式为y=-
| 15x2 |
| 28 |
| 45 |
| 28 |
(4)(3)中的顶点为(
| 3 |
| 2 |
| 135 |
| 112 |
当x=
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 15 |
| 8 |
| 135 |
| 112 |
故(3)的顶点不在直线AB上.
点评:此题考查了二次函数与圆的综合知识,解题时要注意圆的性质,待定系数法的应用,特别是要注意数形结合思想与方程思想的应用.

练习册系列答案
相关题目
 (2013•湖州一模)如图,平面直角坐标系xOy中,Rt△AOB的直角边OA在x轴的正半轴上,点B在第一象限,并且AB=3,OA=6,将△AOB绕点O逆时针旋转90度得到△COD.点P从点C出发(不含点C),沿射线DC方向运动,记过点D,P,B的抛物线的解析式为y=ax2+bx+c(a<0).
(2013•湖州一模)如图,平面直角坐标系xOy中,Rt△AOB的直角边OA在x轴的正半轴上,点B在第一象限,并且AB=3,OA=6,将△AOB绕点O逆时针旋转90度得到△COD.点P从点C出发(不含点C),沿射线DC方向运动,记过点D,P,B的抛物线的解析式为y=ax2+bx+c(a<0).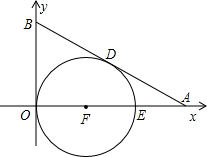 圆与y轴、直线AB分别相切于O、D(如图),若AD=2,AE=1.
圆与y轴、直线AB分别相切于O、D(如图),若AD=2,AE=1.