题目内容
25、当x，y为何值时，多项式x2+y2-4x+6y+28有最小值，求出这个最小值．
分析：把所给多项式整理为两个完全平方式相加的形式，括号外的常数即为多项式的最小值．
解答：解：x2+y2-4x+6y+28=x2-4x+4+y2+6y+9+15=（x-2）2+（y+3）2+15，
∴多项式的最小值为15．
∴多项式的最小值为15．
点评：解决本题的关键是把所给多项式整理为两个完全平方式相加的形式；难点是根据得到的式子判断出所求的最小值．
练习册系列答案
相关题目
宁波港的距离y（千米）与出发时间x（时）之间的函数关系．（船、快艇的长度忽略不计）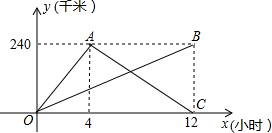
宁波港的距离y（千米）与出发时间x（时）之间的函数关系．（船、快艇的长度忽略不计）