Question

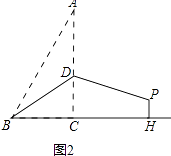
【题目】如图，在扇形OAB中，C是OA的中点，CD⊥OA，CD与 交于点D，以O为圆心，OC的长为半径作 交OB于点E，若OA=4，∠AOB=120°，则图中阴影部分的面积为 ． （结果保留π）

Answer 1

【答案】 π+2
【解析】解：连接O、AD， ∵点C为OA的中点，
∴∠CDO=30°，∠DOC=60°，
∴△ADO为等边三角形，
∴S扇形AOD= = π，
∴S阴影=S扇形AOB﹣S扇形COE﹣（S扇形AOD﹣S△COD）
= ﹣ ﹣（ π﹣ ×2×2 ）
= π﹣ π﹣ π+2
= π+2 ．
故答案为 π+2 ．
连接OD、AD，根据点C为OA的中点可得∠CDO=30°，继而可得△ADO为等边三角形，求出扇形AOD的面积，最后用扇形AOB的面积减去扇形COE的面积，再减去S空白ADC即可求出阴影部分的面积．