Question

一个等边三角形内接于⊙O，这个等边三角形的一边所对的圆周角是

1. A.
   30°
2. B.
   60°
3. C.
   120°
4. D.
   60°或120°

Answer 1

D
分析：根据题意画出图形，根据等边三角形性质求出∠A，根据圆内接四边形性质求出∠D，即可得出答案．
解答：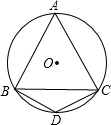
解：∵△ABC是等边三角形，
∴∠A=60°，
∵A、B、D、C四点共圆，
∴∠D+∠A=180°，
∴∠D=120°，
即等边三角形的一边所对的圆周角是60°或120°，
故选D．
点评：本题考查了圆内接四边形性质，等边三角形性质的应用，关键是能求出符合条件的所有情况．