��Ŀ����
��ͼ����ֱ֪�� ��x�ύ�ڵ�A����y�ύ�ڵ�B������AOB�Ƶ�O˳ʱ����ת90���õ���COD��
��x�ύ�ڵ�A����y�ύ�ڵ�B������AOB�Ƶ�O˳ʱ����ת90���õ���COD��

��1����C���������� �����߶�AD�ij������� ����
��2����M��CD�ϣ���CM=OM��������y=x2+bx+c������G��M���������ߵĽ���ʽ��
��3�������E��y���ϣ���λ�ڵ�C���·�����F��ֱ��AC�ϣ���ô�ڣ�2���е����������Ƿ���ڵ�P��ʹ����C��E��F��PΪ������ı��������Σ������ڣ�����������ε��ܳ�l���������ڣ���˵�����ɣ�
�⣺��1����0��3����4��
��2��
��3���������ϴ��ڵ�P��ʹ����C��E��F��PΪ������ı��������Ρ�
��������
�����������1���������ͼ����x�ύ�ڵ�A����y�ύ�ڵ�B�����꣬�����ó�C�������Լ��߶�AD�ij���
�� ��x�ύ�ڵ�A����y�ύ�ڵ�B��
��x�ύ�ڵ�A����y�ύ�ڵ�B��
��y=0ʱ��x=��3��x=0ʱ��y=1��
��A������������3��0����B����������0��1����
��OC=3��DO=1��
���C�������ǣ�0��3�����߶�AD�ij�����4��
��2�����ȵó���M��CD���е㣬���ɵó�M�����꣬�������ô���ϵ��������κ�������ʽ��
��CM=OM�����OCM=��COM��
�ߡ�OCM+��ODM=��COM+��MOD=90�㣬���ODM=��MOD����OM=MD=CM��
���M��CD���е㣬���M������Ϊ�� ��
�� ����
����
��������y=x2+bx+c������C��M��
�� ����ã�
����ã� ��
��
��������y=x2+bx+c�Ľ���ʽΪ�� ��
��
��3���ֱ���ݵ���F�ڵ�C�����ʱ�Լ�����F�ڵ�C���ұ�ʱ�������ı���CFPEΪ���εó����ɡ�
����1����ͼ1������F�ڵ�C�����ʱ���ı���CFEPΪ���Σ�

���FCE=PCE��
�������֪��OA=OC�����ACO=��PCE=45�㡣
���FCP=90�㡣������CFEPΪ�����Ρ�
����P��PH��CE������ΪH��
��Rt��CHPΪ����ֱ�������Ρ�
��CP= CH=
CH= PH��
PH��
���P��x�� ������OH=
������OH= ��PH=x��
��PH=x��
��PH=CH=OC��OH���� ����ã�x1=
����ã�x1= �� x2=0����ȥ����
�� x2=0����ȥ����
��CP= CH=
CH= ��
��
������CFEP���ܳ�lΪ�� ��
��
����2����ͼ2������F�ڵ�C���ұ�ʱ���ı���CFPEΪ���Σ�

��CF=PF��CE��FP��
��ֱ��AC����A����3��0������C��0��3����
��ֱ��AC�Ľ���ʽΪ��y=x+3��
����C��CM��PF������ΪM��
��Rt��CMFΪ����ֱ�������Σ�CM=FM��
�ӳ�PF��x���ڵ�N����PN��x�ᣬ
��PF=FN��PN��
���P��x�� �������F��x��x+3����
�������F��x��x+3����
�� ��
��
�� ����ã�
����ã�
 ��x2=0����ȥ����
��x2=0����ȥ����
�� ��
��
������CFEP���ܳ�lΪ�� ����
����
�������������������δ��ڣ������ܳ�Ϊ ��
�� ��
��

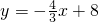 ��x�ύ�ڵ�A����y�ύ�ڵ�B��C���߶�AB���е㣮������y=ax2+bx+c��a��0����O��A���㣬���䶥���������Ϊ
��x�ύ�ڵ�A����y�ύ�ڵ�B��C���߶�AB���е㣮������y=ax2+bx+c��a��0����O��A���㣬���䶥���������Ϊ ��
��
 ��ͼ����ֱ֪��
��ͼ����ֱ֪��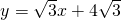 ��x�ᣬy��ֱ���A��B���㣬ֱ��BC��x�ύ�ڵ�C����AB=BC��
��x�ᣬy��ֱ���A��B���㣬ֱ��BC��x�ύ�ڵ�C����AB=BC�� ��ͼ����ֱ֪��
��ͼ����ֱ֪��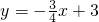 ��x�ύ�ڵ�A����y�ύ�ڵ�B����C�ڷ���������
��x�ύ�ڵ�A����y�ύ�ڵ�B����C�ڷ���������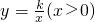 �ϣ���ABC�ǵ���ֱ�������Σ��ҡ�CBA=90�㣮
�ϣ���ABC�ǵ���ֱ�������Σ��ҡ�CBA=90�㣮 ��x�ᡢy��ֱ��ڵ�A��B���߶�ABΪֱ�DZ��ڵ�һ������������Rt��ABC����BAC=90��.
��x�ᡢy��ֱ��ڵ�A��B���߶�ABΪֱ�DZ��ڵ�һ������������Rt��ABC����BAC=90��.