题目内容
 如图,D是半径为2的⊙0上一点,过点D作⊙0的切线交直径AB的延长线于点C,且BC=OB,则弦AD的长为________.
如图,D是半径为2的⊙0上一点,过点D作⊙0的切线交直径AB的延长线于点C,且BC=OB,则弦AD的长为________.
2
分析:连接OD,由切线的性质可得三角形ODB为直角三角形,因为BC=OB,所以OD=OB= OC,所以∠C=30°,利用三角形外角和定理可证明∠A=30°,所以△ADC是等腰三角形,
OC,所以∠C=30°,利用三角形外角和定理可证明∠A=30°,所以△ADC是等腰三角形,
即AD=CD,所以求AD的长转化为求CD的长即可.
解答: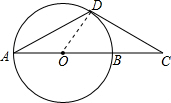 解:连接OD,
解:连接OD,
∵CD是⊙0的切线,
∴OD⊥CD,
∴∠ODC=90°,
∴△ODC是直角三角形,
∵BC=OB,
∴OD=OB= OC,
OC,
∴∠C=30°,
∴∠DOC=60°,
∵OD=2,
∴OC=4,
∴CD=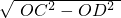 =2
=2 ,
,
∵AO=DO,
∴∠A=∠ADO=30°,
∴∠A=∠C=30°,
∴AD=AC=2 ,
,
故答案为:2 .
.
点评:本题考查了切线的性质,含30度角的直角三角形的性质:在直角三角形中,30°角所对的直角边等于斜边的一半以及勾股定理的运用和等腰三角形的判定和性质,题目简单.

分析:连接OD,由切线的性质可得三角形ODB为直角三角形,因为BC=OB,所以OD=OB=
 OC,所以∠C=30°,利用三角形外角和定理可证明∠A=30°,所以△ADC是等腰三角形,
OC,所以∠C=30°,利用三角形外角和定理可证明∠A=30°,所以△ADC是等腰三角形,即AD=CD,所以求AD的长转化为求CD的长即可.
解答:
 解:连接OD,
解:连接OD,∵CD是⊙0的切线,
∴OD⊥CD,
∴∠ODC=90°,
∴△ODC是直角三角形,
∵BC=OB,
∴OD=OB=
 OC,
OC,∴∠C=30°,
∴∠DOC=60°,
∵OD=2,
∴OC=4,
∴CD=
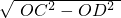 =2
=2 ,
,∵AO=DO,
∴∠A=∠ADO=30°,
∴∠A=∠C=30°,
∴AD=AC=2
 ,
,故答案为:2
 .
.点评:本题考查了切线的性质,含30度角的直角三角形的性质:在直角三角形中,30°角所对的直角边等于斜边的一半以及勾股定理的运用和等腰三角形的判定和性质,题目简单.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
如图,BC是半径为1的⊙O的弦,A为弧BC上一点,M、N分别为BD、AD的中点,则sin∠C的值等于( )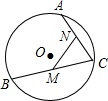

| A、AD | B、BC | C、MN | D、AC |
 如图,
如图, |
| AB |
 |
| BC |
A、s=
| ||||
B、s=
| ||||
C、s=
| ||||
D、s=
|
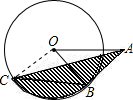 如图,A是半径为2的⊙O外一点,OA=4,AB是⊙O的切线,点B是切点,弦BC∥OA,连接AC,则图中阴影部分的面积为
如图,A是半径为2的⊙O外一点,OA=4,AB是⊙O的切线,点B是切点,弦BC∥OA,连接AC,则图中阴影部分的面积为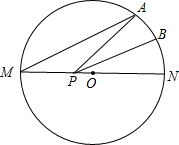 如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,点P是直径MN上一个动点,则PA+PB的最小值为( )
如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,点P是直径MN上一个动点,则PA+PB的最小值为( ) 如图,P是半径为4的⊙O外一点,PA切⊙O于A,PB切⊙O于B,∠APB=60°.
如图,P是半径为4的⊙O外一点,PA切⊙O于A,PB切⊙O于B,∠APB=60°.