题目内容
已知如图，P为⊙O外一点，过点P作⊙O的切线，切点为C，过P，O两点作⊙O的割线交⊙O于A、B两点，且PC=4cm，PA=3cm，则⊙O的半径R= cm．
【答案】分析：根据切割线定理，可得到比例线段，先求出BP的值，再求直径AB，从而求出半径．
解答：解：∵PC是切线，
∴PC2=PA•PB；
又∵PC=4，PA=3，
∴16=3（3+AB），
∴AB=
，
∴半径R=
．
点评：此题主要运用了切割线定理的有关知识来解决问题．
解答：解：∵PC是切线，
∴PC2=PA•PB；
又∵PC=4，PA=3，
∴16=3（3+AB），
∴AB=
，∴半径R=
．点评：此题主要运用了切割线定理的有关知识来解决问题．
练习册系列答案
新课标阶梯阅读训练系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
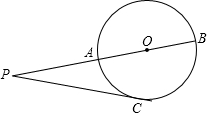已知如图，P为⊙O外一点，过点P作⊙O的切线，切点为C，过P，O两点作⊙O的割线交⊙O于A、B两点，且PC=4cm，PA=3cm，则⊙O的半径R=
已知如图，P为⊙O外一点，过点P作⊙O的切线，切点为C，过P，O两点作⊙O的割线交⊙O于A、B两点，且PC=4cm，PA=3cm，则⊙O的半径R=________cm．
