Question

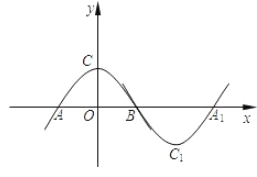
【题目】如图，抛物线与轴于点、（点在点的左侧），与轴交于点．将抛物线绕点旋转，得到新的抛物线，它的顶点为，与轴的另一个交点为．若四边形为矩形，则，应满足的关系式为（ ）

A. B. C. D.

Answer 1

【答案】B

【解析】

先利用抛物线与x轴的交点问题求出A（-，0），B（0），则确定C（0，b），则OA=OB=，再利用中心对称的性质得到∴A1B=AB=2，然后根据射影定理得到OC2=OAOA1，即b2=3，接着变形等式即可得到ab=-3．

解：当y=0时，ax2+b=0，解得x=±，则A（-，0），B（，0），

当x=0时，y=ax2+b=b，则C（0，b），
∴OA=OB=,

∵抛物线l1绕点B顺时针旋转180°，得到新的抛物线l2，它的顶点为C1，与x轴的另一个交点为A1．
∴A1B=AB=2，∵四边形AC1A1C为矩形，
∴∠ACA1=90°，
∴OC2=OAOA1，即b2=3，

∴ab=-3．

故选：B．