题目内容
如图,有一直线y=
x+1,将抛物线y=
x2,沿x轴作左右平移,记平移后的抛物线为C,抛物线C与Y轴交于点E.与直线交于两点,其中一个交点为F,当线段EF∥x轴时,求平移后的抛物线C的表达式.
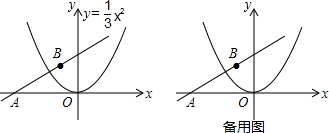
| 1 |
| 3 |
| 1 |
| 3 |
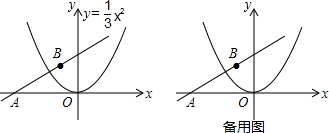
考点:二次函数图象与几何变换
专题:
分析:根据“左加右减、上加下减”的平移规律先设出抛物线C的表达式,即可得出E点的坐标;点E为抛物线C与y轴的交点,点F为直线AB与抛物线C的交点,也可以理解为点E、F都在抛物线C的图象上,若EF∥x轴,那么点E、F必关于抛物线对称轴对称,首先根据点E的坐标和抛物线对称轴方程表示出点F的坐标,再代入直线AB的解析式中进行求解即可.
解答:解:设抛物线C的解析式为y=
(x-t)2,则顶点(t,0),E(0,
t2),
∵EF∥x轴且F在抛物线C上,根据抛物线的对称性可知F(2t,
t2),
把x=2t,y=
t2代入y=
x+1得
×2t+1=
t2,
解得t1=-1,t2=3,
∴抛物线C的解析式为y=
(x+1)2或y=
(x-3)2.
| 1 |
| 3 |
| 1 |
| 3 |
∵EF∥x轴且F在抛物线C上,根据抛物线的对称性可知F(2t,
| 1 |
| 3 |
把x=2t,y=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
解得t1=-1,t2=3,
∴抛物线C的解析式为y=
| 1 |
| 3 |
| 1 |
| 3 |
点评:本题考查了二次函数图象与几何变换,根据EF与x轴平行得到点E、F的纵坐标相等是解题的关键,利用顶点的变化确定抛物线解析式的变化求解更简便.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
下列说法正确的是( )
| A、无限小数都是分数 | ||
B、
| ||
| C、平方根等于本身的数是0 | ||
| D、数轴上的每一个点都表示一个有理数 |
下列各式:-(-3);-|-3|;-32;(-3)4;
,计算结果为负数的有( )
| 3 | -27 |
| A、4个 | B、3个 | C、2个 | D、1个 |
计算:(28a2b2-21ab2)÷7ab的值是( )
| A、4a2-3 |
| B、4a-3 |
| C、4a2-3b |
| D、4a2b-3 |
 如图,是反比例函数y=
如图,是反比例函数y=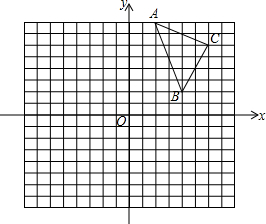 如图,在由边长为1的小正方形组成的网格图中有△ABC,建立平面直角坐标系后,点O的坐标是(0,0).
如图,在由边长为1的小正方形组成的网格图中有△ABC,建立平面直角坐标系后,点O的坐标是(0,0).