题目内容
如图,已知平行四边形ABCD,过A作AM⊥BC于M,交BD于E,过C作CN⊥AD于N,交BD于F,连结AF、CE.
(1)求证:四边形AECF为平行四边形;
(2)当AECF为菱形,M点为BC的中点时,求AB:AE的值.

(1)证明:因为AE⊥BC,所以∠AMB=900,
因为CN⊥AD,所以∠CNA=900.
又因为BC‖AD,所以∠BCN=900.
所以AE∥CF,………………………………………………………………………2分
又由平行得∠ADE=∠CBD,又AD=BC,
所以ΔADE≌△BCF,
所以AE=CF,
所以四边形AECF为平行四边形.…![]() ………………………………………………4分
………………………………………………4分
(2)当AECF为菱形时,连结AC交BF于点0,
则AC与EF互相垂直平分,
 又BO=OD,
又BO=OD,
所以AC与BD互相垂直平分,
所以,四边形ABCD是菱形,……………………6分
所以AB=BC.
因为M是BC的中点,AM⊥BC,
所以,ΔABM≌ΔCAM,
所以,AB=AC,
ΔABC为等边三角形,
∠ABC=600,∠CBD=300. ………………………………………………………8分
在RtΔBCF中,
CF:BC=tan∠CBF=![]() ,
,
又AE=C![]() F,AB=BC,
F,AB=BC,
所以AB:AE=![]() …………………………………………………………………l0分
…………………………………………………………………l0分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 CD的边长a等于点P,Q间的距离.
CD的边长a等于点P,Q间的距离. 如图,已知平行四边形ABCD的对角线AC,BD相交于点O,BD绕点O顺时针旋转交AB,DC于E,F.
如图,已知平行四边形ABCD的对角线AC,BD相交于点O,BD绕点O顺时针旋转交AB,DC于E,F.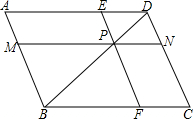 交AB、CD、AD、BC于M、N、E、F,设a=PM•PE,b=PN•PF.
交AB、CD、AD、BC于M、N、E、F,设a=PM•PE,b=PN•PF. 23、如图,已知平行四边形ABCD.
23、如图,已知平行四边形ABCD. 如图,已知平行四边形ABCD,作DE⊥AB,垂足为E,把三角形AED沿AB方向平移AB长个单位长度.
如图,已知平行四边形ABCD,作DE⊥AB,垂足为E,把三角形AED沿AB方向平移AB长个单位长度.