题目内容
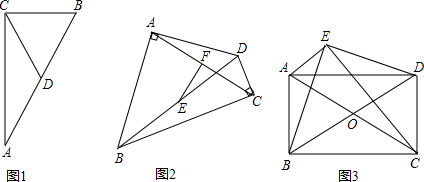
Rt△ABC，CD⊥AB于点D，BD=9，DC=12，则AD=________．
16
分析：利用互余关系证明：∠A=∠BCD，可证Rt△ACD∽Rt△CBD，然后利用相似比，就可求出AD的值．
解答：∵∠A=90°-∠B=∠BCD，
∴Rt△ACD∽Rt△CBD，
∴AD：CD=CD：BD，
即AD：12=12：9，
解得AD=16．
点评：本题考查相似三角形的性质以及相似比的应用．
分析：利用互余关系证明：∠A=∠BCD，可证Rt△ACD∽Rt△CBD，然后利用相似比，就可求出AD的值．
解答：∵∠A=90°-∠B=∠BCD，
∴Rt△ACD∽Rt△CBD，
∴AD：CD=CD：BD，
即AD：12=12：9，
解得AD=16．
点评：本题考查相似三角形的性质以及相似比的应用．
练习册系列答案
相关题目
6、Rt△ABC，CD⊥AB于点D，BD=9，DC=12，则AD=
（2013•郴州）如图，在Rt△ACB中，∠ACB=90°，∠A=25°，D是AB上一点．将Rt△ABC沿CD折叠，使B点落在AC边上的B′处，则∠ADB′等于（ ）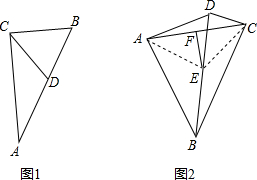
（1）如图1，经历矩形性质的探索过程，你可以发现：直角三角形斜边上的中线等于斜边上的一半．如在Rt△ABC中CD是斜边AB的中线，则CD=