题目内容
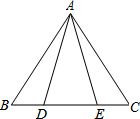如图，△ABE≌△ACD，∠ADB=105°，∠B=60°，则∠BAE=________．
45°
分析：首先根据全等能够三角形的性质可得∠AEB=∠ADE，根据∠ADB=105°可得∠AEB的度数，再利用三角形内角和定理可得答案．
解答：∵△ABE≌△ACD，
∴∠AEB=∠ADE，
∵∠ADB=105°，
∴∠ADE=180°-105°=75°，
∴∠AEB=75°，
∵∠B=60°，
∴∠BAE=180°-60°-75°=45°．
故答案为：45°．
点评：此题主要考查了全等三角形的性质，以及三角形内角和定理，关键是掌握全等三角形的对应角相等．
分析：首先根据全等能够三角形的性质可得∠AEB=∠ADE，根据∠ADB=105°可得∠AEB的度数，再利用三角形内角和定理可得答案．
解答：∵△ABE≌△ACD，
∴∠AEB=∠ADE，
∵∠ADB=105°，
∴∠ADE=180°-105°=75°，
∴∠AEB=75°，
∵∠B=60°，
∴∠BAE=180°-60°-75°=45°．
故答案为：45°．
点评：此题主要考查了全等三角形的性质，以及三角形内角和定理，关键是掌握全等三角形的对应角相等．
练习册系列答案
相关题目
11、如图，△ABE、△ACD都是等边三角形，∠BAC=70°，图中△ACE可以看作由△ADB绕A点（ ）度得到．
27、如图，△ABE和△ACF分别是以△ABC的AB、AC为边的正三角形，CE、BF相交于O．
与AB的延长线交于点P．
如图，△ABE和△ACD有公共点A，∠BAC=∠DAE=90°，AB=AC，AE=AD，延长BE分别交AC、CD于点M、F．求证：