题目内容
已知:如图,C为半圆上一点, |
| AC |
 |
| CE |
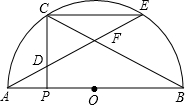 别交PC,CB于点D,F.
别交PC,CB于点D,F.(1)求证:AD=CD;
(2)若DF=
| 5 |
| 4 |
| 3 |
| 4 |
分析:(1)要求证:AD=CD,可以连接AC,转化为证明∠CAD=∠ACD.
(2)已知tan∠ECB=
,就是已知∠DAP的正切值,根据△APC∽△CPB,可以根据相似三角形的对应边的比相等求得.
(2)已知tan∠ECB=
| 3 |
| 4 |
解答: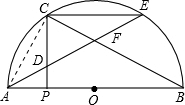 (1)证明:连接AC,
(1)证明:连接AC,
∵
=
,
∴∠CEA=∠CAE.
∵∠CEA=∠CBA,
∴∠CBA=∠CAE.
∵AB是直径,
∴∠ACB=90°.
∴∠ACP+∠PCB=90°,
∵CP⊥AB,
∴∠PCB+∠CBA=90°,
∴∠CBA=∠ACP,
∴∠CAE=∠ACP
∴AD=CD.(4分)
(2)解:∵∠ACB=90°,∠CAE=∠ACP,
∴∠DCF=∠CFD.
∴AD=CD=DF=
.(5分)
∵∠ECB=∠DAP,tan∠ECB=
,
∴tan∠DAP=
=
.(6分)
∵DP2+PA2=DA2
∴DP=
,PA=1.
∴CP=2.(7分)
∵∠ACB=90°,CP⊥AB,
∴△APC∽△CPB.(8分)
∴
=
.
∴PB=4.(9分)
 (1)证明:连接AC,
(1)证明:连接AC,∵
 |
| AC |
 |
| CE |
∴∠CEA=∠CAE.
∵∠CEA=∠CBA,
∴∠CBA=∠CAE.
∵AB是直径,
∴∠ACB=90°.
∴∠ACP+∠PCB=90°,
∵CP⊥AB,
∴∠PCB+∠CBA=90°,
∴∠CBA=∠ACP,
∴∠CAE=∠ACP
∴AD=CD.(4分)
(2)解:∵∠ACB=90°,∠CAE=∠ACP,
∴∠DCF=∠CFD.
∴AD=CD=DF=
| 5 |
| 4 |
∵∠ECB=∠DAP,tan∠ECB=
| 3 |
| 4 |
∴tan∠DAP=
| DP |
| PA |
| 3 |
| 4 |
∵DP2+PA2=DA2
∴DP=
| 3 |
| 4 |
∴CP=2.(7分)
∵∠ACB=90°,CP⊥AB,
∴△APC∽△CPB.(8分)
∴
| AP |
| PC |
| PC |
| PB |
∴PB=4.(9分)
点评:本题主要考查了三角函数的值是有角的大小确定的,以及相似三角形的对应边的比相等.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
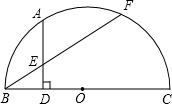 AD于点E.
AD于点E. 点E.
点E.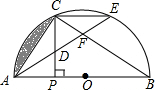 D、F.
D、F. 已知:如图,AB为半圆的直径,弦CD∥AB,∠CAD=30°,若AB长为8cm,求△ACD的面积.
已知:如图,AB为半圆的直径,弦CD∥AB,∠CAD=30°,若AB长为8cm,求△ACD的面积. 已知:如图,AB为半圆的直径,O为圆心,C为半圆上一点,OE⊥弦AC于点D,交⊙O于点E.若AC=8cm,DE=2cm.求OD的长.
已知:如图,AB为半圆的直径,O为圆心,C为半圆上一点,OE⊥弦AC于点D,交⊙O于点E.若AC=8cm,DE=2cm.求OD的长.