题目内容
如图,直角坐标系中,已知A(2,4),B(5,0),动点P从B点出发,沿BO向终点O移动;动点Q从点A点出发,沿AB向终点B移动.两点同时出发,速度均为每秒1个单位.设从出发起运动了x秒.
(1)点P的坐标是(________,________);
(2)点Q的坐标是(________,________);
(3)x为何值时,△APQ是以AP为腰的等腰三角形?

解:(1)x秒点P行走的距离为x,则OP=5-x,
故点P的坐标是(5-x,0);
(2)作AD⊥OB,QE⊥OB,则△BAD∽△BQE,

即 =
= ,
, =
= ,
,
∵AD=4,OD=2,OB=5,
∴BD=3,
∴AB=5,
在x秒Q点行走距离为x,则AQ=x,BQ=5-x,
∴ ,
, ,
,
∴BE=3- x,QE=4-
x,QE=4- x,
x,
∴OE=OB-BE=5-(3- x)=2+
x)=2+ ,
,
则点Q的坐标是(2+ ,4-
,4- );
);
(3)由题意,AP2=(5-x-2)2+42=x2-6x+25,
AQ2= +
+ =x2,
=x2,
PQ2= +
+
= -16x+25.
-16x+25.
若AP=AQ,则x= ;
;
若AP=PQ,则x1= ,x2=0(舍去)
,x2=0(舍去)
故x= 或
或 秒时,△APQ是以AP为腰的等腰三角形.
秒时,△APQ是以AP为腰的等腰三角形.
故答案为(1)点P的坐标是(5-x,0);(2)点Q的坐标是(2+ ,4-
,4- );(3)x=
);(3)x= 或
或 秒时,△APQ是以AP为腰的等腰三角形.
秒时,△APQ是以AP为腰的等腰三角形.
分析:(1)根据P的行走路程可以计算P的坐标;
(2)根据勾股定理分别求Q的横坐标和纵坐标;
(3)根据勾股定理计算AP、AQ的长度,当AP=AQ时,可得△APQ是以AP为腰的等腰三角形.
点评:本题考查了平面直角坐标系中坐标的计算,考查了勾股定理在平面直角坐标系中的运用,本题中根据AP和AQ的表达式和AP=AQ计算x的值是解题的关键.
故点P的坐标是(5-x,0);
(2)作AD⊥OB,QE⊥OB,则△BAD∽△BQE,

即
 =
= ,
, =
= ,
,∵AD=4,OD=2,OB=5,
∴BD=3,
∴AB=5,
在x秒Q点行走距离为x,则AQ=x,BQ=5-x,
∴
 ,
, ,
,∴BE=3-
 x,QE=4-
x,QE=4- x,
x,∴OE=OB-BE=5-(3-
 x)=2+
x)=2+ ,
,则点Q的坐标是(2+
 ,4-
,4- );
);(3)由题意,AP2=(5-x-2)2+42=x2-6x+25,
AQ2=
 +
+ =x2,
=x2,PQ2=
 +
+
=
 -16x+25.
-16x+25.若AP=AQ,则x=
 ;
;若AP=PQ,则x1=
 ,x2=0(舍去)
,x2=0(舍去)故x=
 或
或 秒时,△APQ是以AP为腰的等腰三角形.
秒时,△APQ是以AP为腰的等腰三角形.故答案为(1)点P的坐标是(5-x,0);(2)点Q的坐标是(2+
 ,4-
,4- );(3)x=
);(3)x= 或
或 秒时,△APQ是以AP为腰的等腰三角形.
秒时,△APQ是以AP为腰的等腰三角形.分析:(1)根据P的行走路程可以计算P的坐标;
(2)根据勾股定理分别求Q的横坐标和纵坐标;
(3)根据勾股定理计算AP、AQ的长度,当AP=AQ时,可得△APQ是以AP为腰的等腰三角形.
点评:本题考查了平面直角坐标系中坐标的计算,考查了勾股定理在平面直角坐标系中的运用,本题中根据AP和AQ的表达式和AP=AQ计算x的值是解题的关键.

练习册系列答案
相关题目
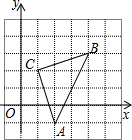 如图,直角坐标系中,△ABC的顶点都在网格点上,其中,A点坐标为(2,-1),则△ABC的面积为
如图,直角坐标系中,△ABC的顶点都在网格点上,其中,A点坐标为(2,-1),则△ABC的面积为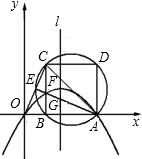 ?若存在,请求出所有这样的点;若不存在,请说明理由.
?若存在,请求出所有这样的点;若不存在,请说明理由. 在如图平面直角坐标系中,△ABC三个顶点A、B、C的坐标分别为A(2,-1),B(1,-3),C(4,-4),
在如图平面直角坐标系中,△ABC三个顶点A、B、C的坐标分别为A(2,-1),B(1,-3),C(4,-4), 如图,直角坐标系中,△ABC的顶点都在网格点上,C点坐标为(1,2),原来△ABC各个顶点纵坐标不变,横坐标都增加2,所得的三角形面积是
如图,直角坐标系中,△ABC的顶点都在网格点上,C点坐标为(1,2),原来△ABC各个顶点纵坐标不变,横坐标都增加2,所得的三角形面积是 在如图的直角坐标系中,将△ABC平移后得到△A′B′C′,它们的个顶点坐标如表所示:
在如图的直角坐标系中,将△ABC平移后得到△A′B′C′,它们的个顶点坐标如表所示: