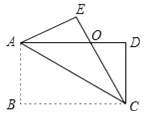
题目内容
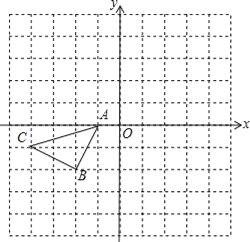
【题目】如图在平面直角坐标系中,已知![]() ,其中
,其中![]() 满足
满足![]() .
.
(1)填空:![]() = _____ ,
= _____ ,![]() = _____ ;
= _____ ;
(2)如果在第三象限内一点![]() ,请用含
,请用含![]() 的式子表示⊿
的式子表示⊿![]() 的面积;
的面积;
(3)若⑵条件下,当![]() 时,在坐标轴上一点
时,在坐标轴上一点![]() ,使得⊿
,使得⊿![]() 的面积与⊿
的面积与⊿![]() 的面积相等,请求出点
的面积相等,请求出点![]() 的坐标.
的坐标.

【答案】(1)a=-1,b= 3; (2)![]() ⊿
⊿![]() =-2m; (3) 点
=-2m; (3) 点![]() 的坐标为:
的坐标为:![]() 、
、![]() 、
、![]() 、
、![]() .
.
【解析】
⑴根据非负数的和为0,则每一个非负数均为0,即可解答;⑵问根据⑴问可以求出边![]() 的长度,用点
的长度,用点 ![]() 的纵坐标可以反映出⊿
的纵坐标可以反映出⊿![]() 的边
的边![]() 上的高,问题可获得解决.⑶根据题意点P可能在坐标轴的正半轴,也有可能在坐标轴的负半轴,进行分类讨论即可作答.
上的高,问题可获得解决.⑶根据题意点P可能在坐标轴的正半轴,也有可能在坐标轴的负半轴,进行分类讨论即可作答.
(1)∵![]() ,且
,且![]()
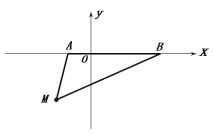
∴![]()
∴![]()
故应填:![]() .
.
(2)过带点![]() 于
于![]() .
.
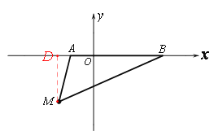
根据⑴问可知![]() ,又
,又![]() 在第三象限.
在第三象限.
∴ ![]()
∴![]() ⊿
⊿![]() =
=![]() .
.
(3)在⑵条件下,当![]() 时,
时,![]() .
.
∴![]() ⊿
⊿![]() 的面积 =
的面积 =![]() ;∴
;∴![]() 的坐标要使⊿
的坐标要使⊿![]() 的面积 =
的面积 =![]() ;
;
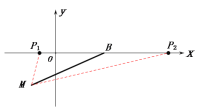
当点P在x轴上,设点![]() 的左标为
的左标为![]() ,则:
,则:
![]() ⊿
⊿![]() =
=![]() 即
即![]() .
.
①当![]() 时,
时,![]() ,解得:
,解得:![]() ; ∴
; ∴![]() .
.
②当![]() 时,
时,![]() ,解得:
,解得:![]() ; ∴
; ∴![]() .
.
当点P在y轴上,设点![]() 的左标为
的左标为![]() ;结合三角形
;结合三角形![]() 的面积为
的面积为![]() ,点
,点![]() 位置有两种情况:
位置有两种情况:
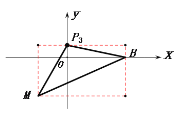
③在直线![]() 与
与![]() 轴交点的上方,且在
轴交点的上方,且在![]() 轴的正半轴,此时的
轴的正半轴,此时的![]() .
.
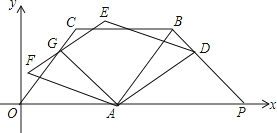
把⊿![]() 放在一个矩形中(见示意图),则:
放在一个矩形中(见示意图),则:
![]() ⊿
⊿![]() =
=![]()
整理得:![]() ,解得:
,解得:![]() ∴
∴![]() .
.
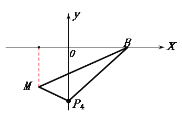
④在![]() 轴的负半轴,且一定在直线
轴的负半轴,且一定在直线![]() 与
与![]() 轴交点的下方,此时的
轴交点的下方,此时的![]() .
.
把⊿![]() 放在一个梯形中(见示意图),则:
放在一个梯形中(见示意图),则:
![]() ⊿
⊿![]() =
=![]()
整理得:![]() ,解得:
,解得:![]() ∴
∴![]() .
.
点![]() 的坐标为:
的坐标为:![]() 、
、![]() 、
、![]() 、
、![]() .
.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目