题目内容
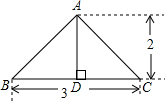
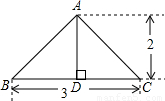
如图所示是一个圆锥在某平面上的正投影,则该圆锥的侧面积是 .
【答案】分析:根据等腰三角形的性质易得圆锥的底面半径,利用勾股定理易得圆锥的母线长,那么圆锥的侧面积=底面周长×母线长÷2.
解答:解:∵BC=3,AD=2,AD⊥BC,AB=AC,
∴CD= BC=
BC= ,
,
在Rt△ACD中,AC= ,
,
∴圆锥的侧面积S=πrl=π× ×
× =
= π.
π.
故答案为: π.
π.
点评:本题考查了勾股定理的运用及圆锥侧面积的求解.
解答:解:∵BC=3,AD=2,AD⊥BC,AB=AC,
∴CD=
 BC=
BC= ,
,在Rt△ACD中,AC=
 ,
,∴圆锥的侧面积S=πrl=π×
 ×
× =
= π.
π.故答案为:
 π.
π.点评:本题考查了勾股定理的运用及圆锥侧面积的求解.

练习册系列答案
相关题目
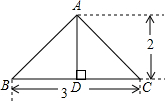 如图所示是一个圆锥在某平面上的正投影,则该圆锥的侧面积是
如图所示是一个圆锥在某平面上的正投影,则该圆锥的侧面积是