题目内容
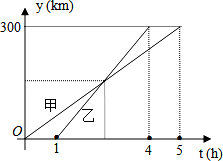
甲、乙两车从 A 城出发匀速行驶至 B 城.在整个行驶过程中,甲、乙两车离开 A 城的距离 y(千 米)与甲车行驶的时间 t(小时)之间的函数关系如图所示.则下列结论:
①A,B 两城相距 300 千米;
②乙车比甲车晚出发 1 小时,却早到 1 小时;
③乙车出发后 2.5 小时追上甲车;
④当甲、乙两车相距 50 千米时,t=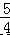 或
或  . 其中正确的结论有( )
. 其中正确的结论有( )
A.1 个 B.2 个 C.3 个 D.4 个
B【考点】一次函数的应用.
【分析】观察图象可判断①②,由图象所给数据可求得甲、乙两车离开 A 城的距离 y 与时间 t 的关 系式,可求得两函数图象的交点,可判断③,再令两函数解析式的差为 50,可求得 t,可判断④, 可得出答案.
【解答】解:
由图象可知 A、B 两城市之间的距离为 300km,甲行驶的时间为 5 小时,而乙是在甲出发 1 小时后 出发的,且用时 3 小时,即比甲早到 1 小时,
∴①②都正确;
设甲车离开 A 城的距离 y 与 t 的关系式为 y 甲=kt, 把(5,300)代入可求得 k=60,
∴y 甲=60t,
设乙车离开 A 城的距离 y 与 t 的关系式为 y 乙=mt+n, 把(1,0)和(4,300)代入可得  ,解得
,解得  ,
,
∴y 乙=100t﹣100,
令 y 甲=y 乙可得:60t=100t﹣100,解得 t=2.5, 即甲、乙两直线的交点横坐标为 t=2.5,
此时乙出发时间为 1.5 小时,即乙车出发 1.5 小时后追上甲车,
∴③不正确;
令|y 甲﹣y 乙|=50,可得|60t﹣100t+100|=50,即|100﹣40t|=50, 当 100﹣40t=50 时,可解得 t=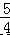 ,
,
当 100﹣40t=﹣50 时,可解得 t= ,
,
又当 t= 时,y 甲=50,此时乙还没出发, 当 t=
时,y 甲=50,此时乙还没出发, 当 t= 时,乙到达 B 城,y 甲=250;
时,乙到达 B 城,y 甲=250;
综上可知当 t 的值为 或
或  或
或  或 t=
或 t= 时,两车相距 50 千米,
时,两车相距 50 千米,
∴④不正确; 综上可知正确的有①②共两个, 故选 B.
【点评】本题主要考查一次函数的应用,掌握一次函数图象的意义是解题的关键,特别注意 t 是甲 车所用的时间.

 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案兰新铁路的通车,圆了全国人民的一个梦,坐上火车去观赏青海门源百里油菜花海,感受大美 青海独特的高原风光,暑假某校准备组织学生、老师到门源进行社会实践,为了便于管理,师生必 须乘坐在同一列高铁上,根据报名人数,若都买一等座单程火车票需 2340 元,若都买二等座单程火
车票花钱最少,则需 1650 元: 西宁到门源的火车票价格如下表
| 运行区间 | 票价 | ||
| 上车站 | 下车站 | 一 等 座 | 二 等 座 |
| 西宁 | 门源 | 36 元 | 30 元 |
(1)参加社会实践的学生、老师各有多少人?
由于各种原因,二等座火车票单程只能买 x 张(参加社会实践的学生人数<x<参加社会实践的总人 数),其余的须买一等座火车票,在保证每位参与人员都有座位坐并且总费用最低的前提下,请你写 出购买火车票的总费用(单程)y 与 x 之间的函数关系式.

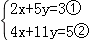
 的积一定是无理数.
的积一定是无理数. 程
程 的两个根,且OA>OB.
的两个根,且OA>OB.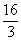 ,求经过D、E两点的直线解析式,并判断△AOE与△AOD是否相似.
,求经过D、E两点的直线解析式,并判断△AOE与△AOD是否相似.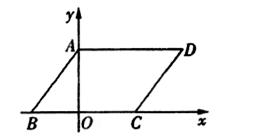 (3)若点M在平面直
(3)若点M在平面直 角坐标系内,则在直线AB上是否存在点F,使以A、C、F、M为顶点的四边形为菱形?若存在,直接写出F点的坐标,若不存在,请说明理由.
角坐标系内,则在直线AB上是否存在点F,使以A、C、F、M为顶点的四边形为菱形?若存在,直接写出F点的坐标,若不存在,请说明理由.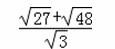
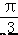 是分数
是分数