题目内容
4.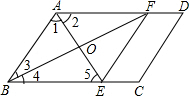 如图,已知在?ABCD中,AE平分∠BAD,即∠1=∠2,BF平分∠ABC,即∠3=∠4,连接EF,求证:四边形ABEF是菱形.
如图,已知在?ABCD中,AE平分∠BAD,即∠1=∠2,BF平分∠ABC,即∠3=∠4,连接EF,求证:四边形ABEF是菱形.
分析 先证明四边形ABEF是平行四边形,再证明邻边相等即可证明.
解答 证明:∵四边形ABCD是平行四边形
∴AD∥BC,
∴∠2=∠5,
∵∠1=∠2,
∴∠1=∠5,
∴AB=BE,同理可得AB=AF,
∴AF=BE,
∴四边形ABEF是平行四边形,
∵AB=AF
∴四边形ABEF是菱形.
点评 本题考查平行四边形的性质与判定、菱形的判定、平行线的性质;熟练掌握平行四边形的判定与性质是解决问题的关键解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.下列图形是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
15.已知|a|=3,则-a的值为( )
| A. | 3 | B. | -3 | C. | ±3 | D. | 9 |
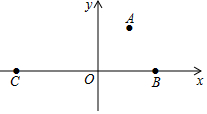
19. 如图,手掌盖住的点的坐标可能是( )
如图,手掌盖住的点的坐标可能是( )
 如图,手掌盖住的点的坐标可能是( )
如图,手掌盖住的点的坐标可能是( )| A. | (3,4) | B. | (-4,3) | C. | (-4,-3) | D. | (3,-4) |
9.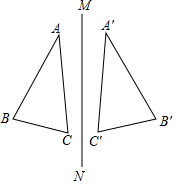 如图,已知△ABC和△A′B′C′关于MN对称,并且AC=5,BC=2,A′B′=4,则△A′B′C′的周长是( )
如图,已知△ABC和△A′B′C′关于MN对称,并且AC=5,BC=2,A′B′=4,则△A′B′C′的周长是( )
 如图,已知△ABC和△A′B′C′关于MN对称,并且AC=5,BC=2,A′B′=4,则△A′B′C′的周长是( )
如图,已知△ABC和△A′B′C′关于MN对称,并且AC=5,BC=2,A′B′=4,则△A′B′C′的周长是( )| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
 已知抛物线y=ax2+bx+2经过A(1,$\frac{5}{4}$),B(2,0)和C三个点.
已知抛物线y=ax2+bx+2经过A(1,$\frac{5}{4}$),B(2,0)和C三个点. 如图,将一块含30°角的直角三角板的直角顶点放在相互平行的两条直线中的一条直线上,若∠1-∠2=18°,则∠3=24°.
如图,将一块含30°角的直角三角板的直角顶点放在相互平行的两条直线中的一条直线上,若∠1-∠2=18°,则∠3=24°.