Question

某校学习小组在开展研究性学习中，对同学们常用的两块直角三角板之间的关系进行了研究，发现了一个有趣的现象：“如果一个三角形中∠A、∠B、∠C所对的边分别为a、b、c，当∠A=2∠B时，有a²-b²=bc”．
（1）请分别在图1和图2中证明上述结论成立；
（2）如图3，△ABC是任意三角形时，上述结论是否成立？若成立，请加以证明；若不成立，请说明理由．

Answer 1

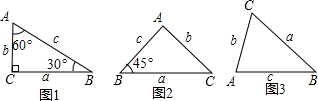
分析：（1）利用，∠C=90°，B=30°求得a、c，从而利用已知条件推出等式成立．
（2）在图3中，作∠CAB的平分线AD交BC于D，利用△ACD∽△BCA由等比性质得．

解答：解：（1）图1中，∠C=90°，B=30°，
∴a=

3

b，c=2b．
∴a²-b²=(

3

b)2-b²=2b²．而bc=b•（2b）=2b²，
∴a²-b²=bc成立．
图2中，∠A=90°，∠B=45°，
∴a²-b²=c²，b=c．
∴bc=c²．
∴a²-b²=bc也成立；

（2）在图3中，作∠CAB的平分线AD交BC于D．
∵∠A=2∠B，
∴∠CAD=∠DAB=∠B，得AD=BD，
∴△ACD∽△BCA，
故

CD

AC

=

AC

BC

=

AD

AB

，
由等比性质，得

CD+AD

AC+AB

=

AC

BC

，
∴

a

b+c

=

b

a

，
即a²-b²=bc．

点评：此题考查学生对相似三角形的判定与性质和勾股定理这一知识点的理解和掌握．