题目内容
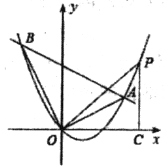
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与一次函数
与一次函数![]() 的图象交于点
的图象交于点![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称.
轴对称.
(1)直接写出点![]() 的坐标;
的坐标;
(2)求点![]() 的坐标(用含
的坐标(用含![]() 的式子表示);
的式子表示);
(3)若![]() 两点中只有一个点在线段
两点中只有一个点在线段![]() 上,直接写出
上,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据对称的性质直接得出点B的坐标即可;
(2)分别联立直线![]() 与一次函数
与一次函数![]() 的解析式,直线
的解析式,直线![]() 与与反比例函数
与与反比例函数![]() 的解析式,求解即可;
的解析式,求解即可;
(3)先求出直线AB的解析式为y=1,再根据若P(m-1,1),Q(m,1)其中只有一个点在线段AB上可得①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,求解即可.
,求解即可.
解:(1)∵A(1,1)与点B关于y轴对称,
∴B的坐标为:(-1,1);
(2)联立直线![]() 与一次函数
与一次函数![]() 的解析式,
的解析式,
得![]() ,
,
解得![]() ,
,
∴P的坐标为(m-1,1),
联立直线![]() 与与反比例函数
与与反比例函数![]() 的解析式,
的解析式,
得 ,
,
解得![]() ,
,
∴Q的坐标为(m,1);
(3)∵A(1,1),B(-1,1),
∴直线AB的解析式为y=1,
若P(m-1,1),Q(m,1)其中只有一个点在线段AB上,则有:
①![]() ,
,
此时不等式组无解;
②![]() ,
,
解得1<m≤2;
③![]() ,
,
解得-1≤m<0;
④![]() ,
,
此时不等式组无解;
综上所述,m的取值范围是![]() 或
或![]() .
.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案【题目】生活垃圾分类回收是实现垃圾减量化和资源化的重要途径和手段.为了解2019年某市第二季度日均可回收物回收量情况,随机抽取该市2019年第二季度的![]() 天数据,整理后绘制成统计表进行分析.
天数据,整理后绘制成统计表进行分析.
日均可回收物回收量(千吨) |
|
|
|
|
| 合计 |
频数 | 1 | 2 |
| 3 |
| |
频率 | 0.05 | 0.10 |
| 0.15 | 1 |
表中![]() 组的频率
组的频率![]() 满足
满足![]() .
.
下面有四个推断:
①表中![]() 的值为20;
的值为20;
②表中![]() 的值可以为7;
的值可以为7;
③这![]() 天的日均可回收物回收量的中位数在
天的日均可回收物回收量的中位数在![]() 组;
组;
④这![]() 天的日均可回收物回收量的平均数不低于3.
天的日均可回收物回收量的平均数不低于3.
所有合理推断的序号是( )
A.①②B.①③C.②③④D.①③④
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中,错误的是( )
A. 抛物线于x轴的一个交点坐标为(﹣2,0)
B. 抛物线与y轴的交点坐标为(0,6)
C. 抛物线的对称轴是直线x=0
D. 抛物线在对称轴左侧部分是上升的