题目内容
 如图,在Rt△ACB中,∠C=90°,BE平分∠CBA交AC于点E,过E作ED⊥AB于D点,当∠A=_____时,ED恰为AB的中垂线
如图,在Rt△ACB中,∠C=90°,BE平分∠CBA交AC于点E,过E作ED⊥AB于D点,当∠A=_____时,ED恰为AB的中垂线
- A.10°
- B.15°
- C.30°
- D.45°
C
分析:在Rt△ABC中结合已知条件分析,要使D为AB的中点,则三角形ABE应是等腰三角形即可.
解答:当∠A=30°时,ED恰为AB的中垂线,理由是:
∵∠A=30°,∠C=90°,
∴∠CBA=60°,
∴∠EBA=∠EBC= ∠CBA=
∠CBA= ×60°=30°,
×60°=30°,
∴ED⊥AB,
∴∠A=∠EBA,
∴EA=EB,
∵ED⊥AB,
∴ED平分AB,
∴ED恰为AB的中垂线.
故选C.
点评:本题主要考查等腰三角形的基本性质;得到三角形ABE应是等腰三角形是正确解答本题的关键.
分析:在Rt△ABC中结合已知条件分析,要使D为AB的中点,则三角形ABE应是等腰三角形即可.
解答:当∠A=30°时,ED恰为AB的中垂线,理由是:
∵∠A=30°,∠C=90°,
∴∠CBA=60°,
∴∠EBA=∠EBC=
 ∠CBA=
∠CBA= ×60°=30°,
×60°=30°,∴ED⊥AB,
∴∠A=∠EBA,
∴EA=EB,
∵ED⊥AB,
∴ED平分AB,
∴ED恰为AB的中垂线.
故选C.
点评:本题主要考查等腰三角形的基本性质;得到三角形ABE应是等腰三角形是正确解答本题的关键.

练习册系列答案
相关题目
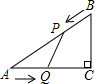 如图,在Rt△ACB中,∠C=90°AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<2).根据以上信息,解答下列问题:
如图,在Rt△ACB中,∠C=90°AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<2).根据以上信息,解答下列问题: 如图:在Rt△ACB中,∠C=90°,AC=8,BC=6,CD是斜边AB上的高.若点P在线段DB上,连接CP,sin∠APC=
如图:在Rt△ACB中,∠C=90°,AC=8,BC=6,CD是斜边AB上的高.若点P在线段DB上,连接CP,sin∠APC= 如图,在Rt△ACB中,∠C=90゜,点O为AB的中点,OE⊥OF交AC于E点、交BC于F点,EM⊥AB,FN⊥AB,垂足分别为M、N,
如图,在Rt△ACB中,∠C=90゜,点O为AB的中点,OE⊥OF交AC于E点、交BC于F点,EM⊥AB,FN⊥AB,垂足分别为M、N, 如图,在Rt△ACB中,∠C=90°,BE平分∠CBA交AC于点E,过E作ED⊥AB于D点,当∠A=
如图,在Rt△ACB中,∠C=90°,BE平分∠CBA交AC于点E,过E作ED⊥AB于D点,当∠A= 如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点,将Rt△ABC沿CD折叠,使点B落在AC边上的B′处,则∠ADB′等于
如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点,将Rt△ABC沿CD折叠,使点B落在AC边上的B′处,则∠ADB′等于