题目内容
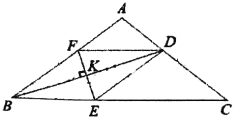
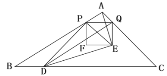
【题目】如图,在![]() 中,
中,![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒
以每秒![]() 个单位长度的速度向终点
个单位长度的速度向终点![]() 运动,过
运动,过![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,以
,以![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,同时以
,同时以![]() 为边向下作正方形
为边向下作正方形![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() 秒
秒![]() .
.
(1)点![]() 到直线
到直线![]() 的距离______________;(用含
的距离______________;(用含![]() 的代数式表示)
的代数式表示)
(2)当点![]() 落在落在
落在落在![]() 上时,求
上时,求![]() 的值;
的值;
(3)设平行四边形![]() 与正方形
与正方形![]() 重叠部分的面积为
重叠部分的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并求出
之间的函数关系式,并求出![]() 的最大值.
的最大值.
(4)设![]() ,当
,当![]() 时,直接写出
时,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() t;(2)t=
t;(2)t=![]() ;(3)S=
;(3)S= .S最大=
.S最大=![]() ;(4)t的值为1≤t≤
;(4)t的值为1≤t≤![]() 或2≤t<3.
或2≤t<3.
【解析】
(1)如图1中,作AH⊥EF于H,交PQ于J.解直角三角形求出JH,AJ即可解决问题.
(2)如图2中,当点D在PF上时,根据BD=PBcos∠B,构建方程即可解决问题.
(3)分两种情形分别求解:①如图3中,当0<t≤![]() 时,重叠部分是△PGQ,②如图4中,当
时,重叠部分是△PGQ,②如图4中,当![]() <t<3时,重叠部分四边形PQDG.
<t<3时,重叠部分四边形PQDG.
(4)分两种情形:①如图5中,作DH∥PE交AB于H,连接EH.由DH∥PE,推出S△PED=S△PEH,推出S△PDE:S△APE=S△PHE:S△APE=PH:PA=m,由此构建不等式即可解决问题.②如图6中,作DH∥PE交AB于H,连接EH.构建不等式即可解决问题.
解:(1)如图1中,作AH⊥EF于H,交PQ于J.
∵PQ∥BC,
∴![]() ,
,
∴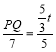 ,
,
∴PQ=![]() t,
t,
∵四边形PQEF是正方形,
∴∠QPF=∠F=90°,
∵AH⊥EF,
∴∠FHJ=90°,
∴四边形PFHJ是矩形,
∴JH=PF=PQ=![]() t,
t,
在Rt△APJ中,AJ=PAsin∠APJ=![]() =t,
=t,
∴AH=AJ+JH=t+![]() t.
t.
(2)如图2中,当点D在PF上时,则有BD=PBcos∠B,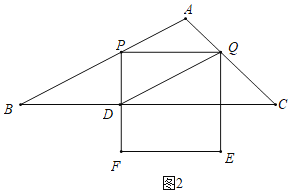
∵四边形PQDB是平行四边形,
∴BD=PQ,
∴(5-![]() t,
t,
解得t=![]() .
.
(3)①如图3中,当0<t≤![]() 时,重叠部分是△PGQ,S=
时,重叠部分是△PGQ,S=![]() t2.
t2.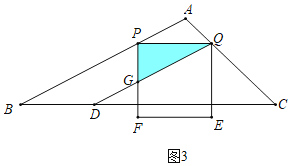
②如图4中,当![]() <t<3时,重叠部分四边形PQDG,
<t<3时,重叠部分四边形PQDG,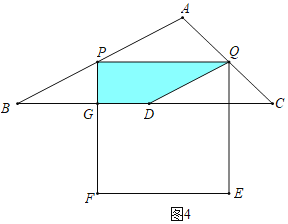
S=S平行四边形PQDB-S△PBG=![]() =-3t2+11t-6.
=-3t2+11t-6.
综上所述,S= .
.
第一种情况,当t=![]() 时,S最大=
时,S最大=![]() .第二种情况,当t=
.第二种情况,当t=![]() 时,S最大=
时,S最大=![]() .
.
综上,S最大=![]() .
.
(4)①如图5中,作DH∥PE交AB于H,连接EH.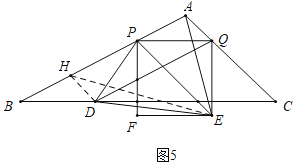
∵DH∥PE,
∴S△PED=S△PEH,
∴S△PDE:S△APE=S△PHE:S△APE=PH:PA=m,
由题意易知:PE∥AC∥DH,
∴BD:BC=BH:BA,
∴![]() t:7=BH:5,
t:7=BH:5,
∴BH=![]() t,
t,
∴PH=5-![]() t-
t-![]() t=5-
t=5-![]() t.
t.
∴m=(5-![]() t):
t):![]() t,
t,
∵![]() ≤m≤1时,
≤m≤1时,
∴![]() ≤
≤![]() ≤1,
≤1,
解得:1≤t≤![]() .
.
②如图6中,作DH∥PE交AB于H,连接EH.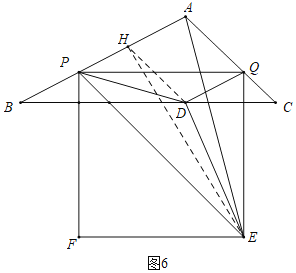
同法可得:∴ ≤1,
≤1,
解得:2≤t≤3.
综上所述,满足条件的t的值为1≤t≤![]() 或2≤t≤3.
或2≤t≤3.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案