题目内容
 如图,直角坐标系中,点A的坐标为(a,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>a>0),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.
如图,直角坐标系中,点A的坐标为(a,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>a>0),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.(1)求证:OC=AD.
(2)随着点C位置的变化,点E的位置是否会发生变化?若没有变化,求出点E的坐标;若有变化,请说明理由.
(3)当C点运动到使OA:AC=1:3时,求出此时D点的坐标.
分析:(1)根据题意可知,BD=BC、∠OBA=∠CBD=60°、BA=OB,便可推出△BOC≌△BAD,即可得结论;
(2)不会发生变化,根据(1)容易得到∠OAE=60°,从而得到E的坐标是固定,为(0,
);
(3)作DM⊥y轴,根据(1)(2)的结论可以推出ED=6a,MD=3a,OM=2
a,即可推出D点的坐标.
(2)不会发生变化,根据(1)容易得到∠OAE=60°,从而得到E的坐标是固定,为(0,
| 3 |
(3)作DM⊥y轴,根据(1)(2)的结论可以推出ED=6a,MD=3a,OM=2
| 3 |
解答:(1)证明:∵△AOB和△CBD是等边三角形,
∴OB=AB,∠OBA=∠OAB=60°,
∵BC=BD,∠CBD=60°,
∴∠OBA+∠ABC=∠CBD+∠ABC,
即∠OBC=∠ABD,
在△OBC和△ABD中,
OB=AB,∠OBC=∠ABD,BC=BD,
∴△OBC≌△ABD,
∴OC=AD.
(2)解:E点的位置不会发生变化,
∵△OBC≌△ABD,
∵∠BAD=∠BOC=60°,
又∵∠OAB=60°,
∴∠OAE=180°-∠OAB-∠BAD=60°,
∴Rt△OEA中,AE=2OA=2a,
∴OE=
a,
∴点E的位置不会发生变化,E的坐标为E(0,
a);
(3)解:作DM⊥y轴,
∵∠MED=30°,OA=a,OA:AC=1:3,AE=2a,AD=OC,
∴ED=6a,
∴MD=3a,
∴EM=3
a,
∴OM=2
a,
∴D点的坐标为(3a,-2
a).
∴OB=AB,∠OBA=∠OAB=60°,
∵BC=BD,∠CBD=60°,
∴∠OBA+∠ABC=∠CBD+∠ABC,
即∠OBC=∠ABD,
在△OBC和△ABD中,
OB=AB,∠OBC=∠ABD,BC=BD,
∴△OBC≌△ABD,
∴OC=AD.
(2)解:E点的位置不会发生变化,
∵△OBC≌△ABD,
∵∠BAD=∠BOC=60°,
又∵∠OAB=60°,
∴∠OAE=180°-∠OAB-∠BAD=60°,
∴Rt△OEA中,AE=2OA=2a,

∴OE=
| 3 |
∴点E的位置不会发生变化,E的坐标为E(0,
| 3 |
(3)解:作DM⊥y轴,
∵∠MED=30°,OA=a,OA:AC=1:3,AE=2a,AD=OC,
∴ED=6a,
∴MD=3a,
∴EM=3
| 3 |
∴OM=2
| 3 |
∴D点的坐标为(3a,-2
| 3 |
点评:本题主要考查全等三角形的判定和性质、等边三角形的性质、坐标与几何图形的关系、勾股定理等知识点,解题的关键在于求证△OBC≌△ABD,结合题意作辅助线构建直角三角形.

练习册系列答案
相关题目
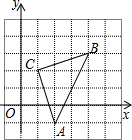 如图,直角坐标系中,△ABC的顶点都在网格点上,其中,A点坐标为(2,-1),则△ABC的面积为
如图,直角坐标系中,△ABC的顶点都在网格点上,其中,A点坐标为(2,-1),则△ABC的面积为 ?若存在,请求出所有这样的点;若不存在,请说明理由.
?若存在,请求出所有这样的点;若不存在,请说明理由. 在如图平面直角坐标系中,△ABC三个顶点A、B、C的坐标分别为A(2,-1),B(1,-3),C(4,-4),
在如图平面直角坐标系中,△ABC三个顶点A、B、C的坐标分别为A(2,-1),B(1,-3),C(4,-4), 如图,直角坐标系中,△ABC的顶点都在网格点上,C点坐标为(1,2),原来△ABC各个顶点纵坐标不变,横坐标都增加2,所得的三角形面积是
如图,直角坐标系中,△ABC的顶点都在网格点上,C点坐标为(1,2),原来△ABC各个顶点纵坐标不变,横坐标都增加2,所得的三角形面积是 在如图的直角坐标系中,将△ABC平移后得到△A′B′C′,它们的个顶点坐标如表所示:
在如图的直角坐标系中,将△ABC平移后得到△A′B′C′,它们的个顶点坐标如表所示: