题目内容
如图，在⊙O中，D、E分别为半径OA、OB上的点，且AD=BE．点C为弧AB上一点，连接CD、CE、CO，∠AOC=∠BOC．
求证：CD=CE．
证明：∵OA=OB AD=BE，
∴OA-AD=OB-BE，即OD=OE．
在△ODC和△OEC中，
，
∴△ODC≌△OEC（SAS）．
∴CD=CE．
分析：证CD和CE所在的三角形全等即可．
点评：两条线段在不同的三角形中要证明相等时，通常是利用全等来进行证明．
∴OA-AD=OB-BE，即OD=OE．
在△ODC和△OEC中，
，∴△ODC≌△OEC（SAS）．
∴CD=CE．
分析：证CD和CE所在的三角形全等即可．
点评：两条线段在不同的三角形中要证明相等时，通常是利用全等来进行证明．
练习册系列答案
导学全程练创优训练系列答案
相关题目
19、如图，在△ABC中，CD⊥AB于D，FG⊥AB于G，ED∥BC，试说明∠1=∠2，以下是证明过程，请填空：
如图，在△ABC中，已知AB=AC，∠BAC=90°，D是BC上一点，EC⊥BC，EC=BD，DF=FE．求证：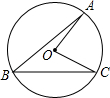
如图，在⊙O中，∠ABC=40°，则∠AOC=
如图，在△ABC中，∠B，∠C的外角平分线相交于点O，若∠A=74°，则∠O=
15、如图，在△ABC中，AQ=PQ，PR=PS，PS⊥AC于S，PR⊥AB于R，则以下结论中：（1）AS=AR；（2）△BRP∽△QSP；（3）PQ∥AB中，正确的有