Question

【题目】在Rt△ABC中，∠CAB=90°，AC=AB=6，D，E分别是AB，AC的中点，若等腰Rt△ADE绕点A逆时针旋转，得到Rt△AD1E1，设旋转角为α（0＜α≤180°），记直线BD1与CE1的交点为P．

（1）如图1，当α=90°时，线段BD1的长等于　　，线段CE1的长等于　　；

（2）如图2，当α=135°时，设直线BD1与CA的交点为F，求证：BD1=CE1，且BD1⊥CE1；

（3）点P到AB所在直线的距离的最大值是　　．

Answer 1

【答案】（1）当α=90°时，线段BD1的长等于，线段CE1的长等于；

（2）证明见解析；

（3）点P到AB所在直线的距离的最大值是.

【解析】试题分析：（1）利用等腰直角三角形的性质结合勾股定理分别得出BD1的长和E1C的长；
（2）根据旋转的性质得出，∠D1AB=∠E1AC=135°，进而求出△D1AB≌△E1AC（SAS），即可得出答案；（3）首先作PG⊥AB，交AB所在直线于点G，则D1，E1在以A为圆心，AD为半径的圆上，当B D1所在直线与⊙A相切时，直线B D1与C E1的交点P到直线AB的距离最大，此时四边形A D1P E1是正方形，进而求出PG的长．

试题解析：（1）∵∠CAB=90°，AC=AB=6，D，E分别是边AB，AC的中点，

∴AE=AD=3，

∵等腰Rt△ADE绕点A逆时针旋转，得到等腰Rt△AD1E1，设旋转角为α（0＜α≤180°），

∴当α=90°时，AE1=3，∠E1AE=90°，

∴BD1==3，E1C==3；

故答案为：3，3；

（2）证明：当α=135°时，如图2，连接CE1，

∵Rt△AD1E是由Rt△ADE绕点A逆时针旋转135°得到，

∴AD1=AE1，∠D1AB=∠E1AC=135°，

在△D1AB和△E1AC中

，

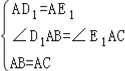∴△D1AB≌△E1AC（SAS），

∴BD1=CE1，且∠D1BA=∠E1CA，

记直线BD1与AC交于点F，

∴∠BFA=∠CFP，

∴∠CPF=∠FAB=90°，

∴BD1⊥CE1；

（3）解：如图3，作PG⊥AB，交AB所在直线于点G，

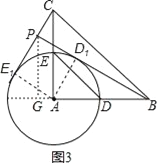
∵D1，E1在以A为圆心，AD为半径的圆上，

∴当BD1所在直线与⊙A相切时，直线BD1与CE1的交点P到直线AB的距离最大，

此时四边形AD1PE1是正方形，PD1=3，则BD1==3，

故∠ABP=30°，

则PB=3+3，

故点P到AB所在直线的距离的最大值为：PG=，

故答案为：．