题目内容
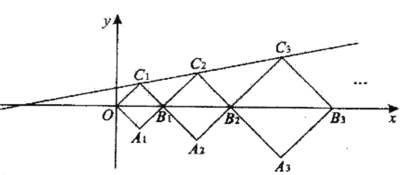
【题目】如图，在平面直角坐标系中，正方形OA1B1C1，B1A2B2C2，B2A3B3C3，···的顶点B1，B2，B3，···在x轴上，顶点C1，C2，C3···在直线y=kx+b上，若正方形OA1B1C1，B1A2B2C2的对角线OB1=2，B1B2=3, 则点C5的纵坐标是_____．
【答案】（
，
）
【解析】
利用正方形性质，求得C1、C2坐标，利用待定系数法求得函数关系式，再求C3坐标，根据C1、C2、C3坐标找出纵坐标规律，求得C5纵坐标，代入关系式，求得C5坐标即可.
如图：根据正方形性质可知：
OB1=2，B1B2=3
C1坐标为（1,1），C2坐标为（
，
）
将C1、C2坐标代入y=kx+b
解得：
所以该直线函数关系式为
设
,则
坐标为（1+2+a，a）
代入函数关系式为，
得：
，解得：
则C3（
，
）
则C1（1,1），C2（，），C3（，）
找出规律：C4纵坐标为
，C5纵坐标为
将C5纵坐标代入关系式，即可得：C5（，）
练习册系列答案
轻松暑假总复习系列答案
相关题目
【题目】2019年4月23日是第24个世界读书日．为了推进中华传统文化教育，营造浓郁的读书氛围，某校举办了“让读书成为习惯，让书香飘满校园”主题活动，为此特为七年级两个班级订购了一批新的图书．七年级两个班级订购图书的情况如下表：
四大名著/套 | 老舍文集/套 | 总费用/元 | |
七年级（1）班 | 2 | 4 | 460 |
七年级（2）班 | 3 | 2 | 530 |
（1）求四大名著和老舍文集每套各是多少元？
（2）学校准备再购买四大名著和老舍文集共10套，总费用不超过800元，求学校最多能买几套四大名著？
