题目内容
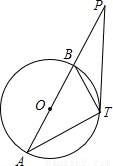
 如图,点在⊙O的直径AB交TP于P,若PA=18,PT=12,PB=8.
如图,点在⊙O的直径AB交TP于P,若PA=18,PT=12,PB=8.(1)求证:△PTB∽△PAT;
(2)求证:PT为⊙O的切线;
(3)在
 | AT |
分析:(1)根据题意有切割线定理易得
=
,∠P为公共角;故可得△PTB∽△PAT;
(2)连接OT,根据勾股定理易得在△ABC中,∠PTO=90°;故PT为⊙O的切线;
(3)假设存在,根据题意推导可得.
| PT |
| PB |
| PA |
| PT |
(2)连接OT,根据勾股定理易得在△ABC中,∠PTO=90°;故PT为⊙O的切线;
(3)假设存在,根据题意推导可得.
解答: (1)证明:∵∠P=∠P,
(1)证明:∵∠P=∠P,
∵PT2=PA•PB,
∴
=
.
∴△PTB∽△PAT.
(2)证明:连接OT,
∵PO2-PT2=OT2,
∴在△ABC中,∠PTO=90°.
∵T为⊙O上一点,
∴PT为⊙O的切线.
(3)在AT弧上存在一点C,使得BT2=8TC
证明:∵∠ABT 是△PBT的一个外角
∴∠ABT>∠P
过点B作BC交AT弧于点C,使∠CBT=∠P
连OT,则OT⊥PT,
∴∠1+∠PTB=90°,
而∠1+∠2=90°,∠2=∠A,
∴∠PTB=∠A,
而∠A=∠C,
∴∠PTB=∠C,
∴△PBT∽△BTC
∴BT:TC=PB:BT
又∵PB=8,
∴BT2=8TC,即在AT弧上存在一点C,使得BT2=8TC.
 (1)证明:∵∠P=∠P,
(1)证明:∵∠P=∠P,∵PT2=PA•PB,
∴
| PT |
| PB |
| PA |
| PT |
∴△PTB∽△PAT.
(2)证明:连接OT,
∵PO2-PT2=OT2,
∴在△ABC中,∠PTO=90°.
∵T为⊙O上一点,
∴PT为⊙O的切线.
(3)在AT弧上存在一点C,使得BT2=8TC

证明:∵∠ABT 是△PBT的一个外角
∴∠ABT>∠P
过点B作BC交AT弧于点C,使∠CBT=∠P
连OT,则OT⊥PT,
∴∠1+∠PTB=90°,
而∠1+∠2=90°,∠2=∠A,
∴∠PTB=∠A,
而∠A=∠C,
∴∠PTB=∠C,
∴△PBT∽△BTC
∴BT:TC=PB:BT
又∵PB=8,
∴BT2=8TC,即在AT弧上存在一点C,使得BT2=8TC.
点评:本题考查了切线的判定,相似三角形的判定,及圆周角定理等知识点的综合运用.

练习册系列答案
相关题目
 如图,点在⊙O的直径AB交TP于P,若PA=18,PT=12,PB=8.
如图,点在⊙O的直径AB交TP于P,若PA=18,PT=12,PB=8. 上是否存在一点C,使得BT2=8TC?若存在,请证明;若不存在,请说明理由.
上是否存在一点C,使得BT2=8TC?若存在,请证明;若不存在,请说明理由.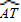 上是否存在一点C,使得BT2=8TC?若存在,请证明;若不存在,请说明理由.
上是否存在一点C,使得BT2=8TC?若存在,请证明;若不存在,请说明理由.
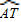 上是否存在一点C,使得BT2=8TC?若存在,请证明;若不存在,请说明理由.
上是否存在一点C,使得BT2=8TC?若存在,请证明;若不存在,请说明理由.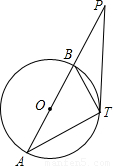
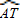 上是否存在一点C,使得BT2=8TC?若存在,请证明;若不存在,请说明理由.
上是否存在一点C,使得BT2=8TC?若存在,请证明;若不存在,请说明理由.