题目内容
已知D是△ABC的边BC上的一点，∠BAD=∠C，那么下列结论中正确的是（ ）
| A、AC2=CD•CB | B、AB2=BD•BC | C、AD2=BD•CD | D、BD2=AD•CD |
分析：由已知条件：∠BAD=∠C、∠B=∠B，可判定△BAD∽△BCA；再根据相似三角形的性质进行判断．
解答：解：∵∠BAD=∠C，∠B=∠B，
∴△BAD∽△BCA；
∴
=
，即AB2=BD•BC；
故选B．
∴△BAD∽△BCA；
∴
| AB |
| BC |
| BD |
| AB |
故选B．
点评：此题主要考查的是相似三角形的判定和性质；能够发现隐含条件公共角∠B是解答此题的关键．
练习册系列答案
相关题目
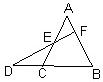16、如图，已知D是△ABC的边BC延长线上一点，DF⊥AB于点F，交AC于点E，∠A=40°，∠D=30°，则∠ACB的度数
如图，已知D是△ABC的边AB上一点，CE∥AB，DE交AC于点O，且OA=OC，猜想线段CD与线段AE的大小关系和位置关系，并加以证明．
如图所示，已知AD是△ABC的边BC上的中线．
30°．