题目内容
如图,在△ABC中,∠BAC=90°,AC=3cm,AB=4cm,AD⊥BC于D,与BD等长的线段EF在边BC上沿BC方向以1cm/s的速度向终点C运动(运动前EF与BD重合),过E,F分别作BC的垂线交直角边于P,Q两点,设EF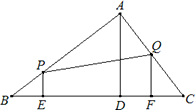 运动的时间为x(s).
运动的时间为x(s).
(1)若△BEP的面积为ycm2,求y关于x的函数解析式,并写出自变量x的取值范围;
(2)线段EF运动过程中,四边形PEFQ有可能成为矩形吗?若有可能,求出此时x的值;若不可能,说明理由;
(3)x为何值时,以A,P,Q为顶点的三角形与△ABC相似?
解:(1)∵PE⊥BC,∠BAC=90°,
∴∠PEB=∠BAC,
∵∠B=∠B,
∴△BPE∽△ABC,
∴ 即
即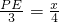 ,
,
∴PE= ,
,
∴y=S△BEP= BE•PE=
BE•PE= •
• =
= ,
,
即y= .
.
在Rt△ABC中,∠BAC=90,AD⊥BC
∵AB=4,AC=3,
∴BC=5,BD= ,DC=
,DC= ,
,
∵0≤BE≤DC,
∴0≤x≤ .
.
答:y关于x的函数解析式是y= x2,自变量x的取值范围是0≤x≤
x2,自变量x的取值范围是0≤x≤ .
.
(2)有可能.
当四边形PEFQ是矩形时,有PE=QF,
由已知得PE= ,
,
与求PE类似可求出QF=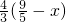 ,
,
∴ =
=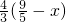 ,
,
解得x=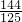 ,
,
∴当x=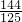 时,四边形PEFQ是矩形.
时,四边形PEFQ是矩形.
(3)分2种情形:
当∠APQ=∠B时,△APQ∽△ABC,
且四边形PEFQ是矩形,此时x=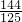 ,
,
当∠APQ=∠C时,
由三角形面积公式得: ×AC×AB=
×AC×AB= BC×AD,
BC×AD,
AC=3,AB=4,BC=5,
∴AD= ,
,
在Rt△ADB中,AB=4,AD= ,由勾股定理得:BD=
,由勾股定理得:BD= ,
,
∴EF=BD= ,
,
∴CF=5-x- =
= -x,
-x,
cos∠C= =
=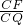 ,
,
CQ= CF=
CF= (
( -x)=3-
-x)=3- x,
x,
∴AQ=3-(3- x)=
x)= x,
x,
∵△AQP∽△ABC,
∴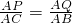 ,
,
即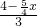 =
=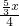 ,
,
解得 x= ,
,
∴当x=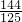 或
或 时,以A,P,Q为顶点的三角形与△ABC相似.
时,以A,P,Q为顶点的三角形与△ABC相似.
分析:(1)证△BPE∽△ABC,得到比例式 ,代入求出即可;
,代入求出即可;
(2)根据矩形的性质得出PE=QF,把PE和QF的值代入求出即可;
(3)由(2)求出x,再∠APQ=∠C,证△AQP∽△ABC相似,得出比例式,求出即可;
点评:本题主要考查对矩形的性质和判定,相似三角形的性质和判定等知识点的理解和掌握,能综合运用性质进行推理和计算是解此题的关键.

∴∠PEB=∠BAC,
∵∠B=∠B,
∴△BPE∽△ABC,
∴
 即
即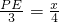 ,
,∴PE=
 ,
,∴y=S△BEP=
 BE•PE=
BE•PE= •
• =
= ,
,即y=
 .
.在Rt△ABC中,∠BAC=90,AD⊥BC
∵AB=4,AC=3,
∴BC=5,BD=
 ,DC=
,DC= ,
,∵0≤BE≤DC,
∴0≤x≤
 .
.答:y关于x的函数解析式是y=
 x2,自变量x的取值范围是0≤x≤
x2,自变量x的取值范围是0≤x≤ .
.(2)有可能.
当四边形PEFQ是矩形时,有PE=QF,
由已知得PE=
 ,
,与求PE类似可求出QF=
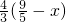 ,
,∴
 =
=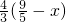 ,
,解得x=
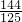 ,
,∴当x=
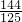 时,四边形PEFQ是矩形.
时,四边形PEFQ是矩形.(3)分2种情形:

当∠APQ=∠B时,△APQ∽△ABC,
且四边形PEFQ是矩形,此时x=
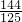 ,
,当∠APQ=∠C时,
由三角形面积公式得:
 ×AC×AB=
×AC×AB= BC×AD,
BC×AD,AC=3,AB=4,BC=5,
∴AD=
 ,
,在Rt△ADB中,AB=4,AD=
 ,由勾股定理得:BD=
,由勾股定理得:BD= ,
,∴EF=BD=
 ,
,∴CF=5-x-
 =
= -x,
-x,cos∠C=
 =
=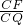 ,
,CQ=
 CF=
CF= (
( -x)=3-
-x)=3- x,
x,∴AQ=3-(3-
 x)=
x)= x,
x,∵△AQP∽△ABC,
∴
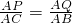 ,
,即
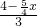 =
=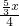 ,
,解得 x=
 ,
,∴当x=
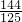 或
或 时,以A,P,Q为顶点的三角形与△ABC相似.
时,以A,P,Q为顶点的三角形与△ABC相似.分析:(1)证△BPE∽△ABC,得到比例式
 ,代入求出即可;
,代入求出即可;(2)根据矩形的性质得出PE=QF,把PE和QF的值代入求出即可;
(3)由(2)求出x,再∠APQ=∠C,证△AQP∽△ABC相似,得出比例式,求出即可;
点评:本题主要考查对矩形的性质和判定,相似三角形的性质和判定等知识点的理解和掌握,能综合运用性质进行推理和计算是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 20、如图,在△ABC中,∠BAC=45°,现将△ABC绕点A逆时针旋转30°至△ADE的位置,使AC⊥DE,则∠B=
20、如图,在△ABC中,∠BAC=45°,现将△ABC绕点A逆时针旋转30°至△ADE的位置,使AC⊥DE,则∠B= 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为 2、如图,在△ABC中,DE∥BC,那么图中与∠1相等的角是( )
2、如图,在△ABC中,DE∥BC,那么图中与∠1相等的角是( ) 如图,在△ABC中,AB=AC,且∠A=100°,∠B=
如图,在△ABC中,AB=AC,且∠A=100°,∠B=