题目内容
【题目】如图，在矩形ABCD中，AB=4，AD=6，点F是AB的中点，E为BC边上一点，且EF⊥ED，连结DF，M为DF的中点，连结MA，ME．若AM⊥ME，则AE的长为（ ）
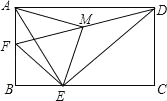
A．5 B．2
C．2
D．4
【答案】B
【解析】
试题分析：设BE=x，则EC=6﹣x，由△EBF∽△DCE，得
，列出方程求出x，即可解决问题．
设BE=x，则EC=6﹣x， ∵EF⊥ED， ∴∠FED=90°， ∴∠FEB+∠DEC=90°，
∵∠DEC+∠EDC=90°， ∴∠FEB=∠EDC， ∵∠B=∠C=90°， ∴△EBF∽△DCE，
∴， ∴
，解得x=2或4（舍弃）， 当x=2时，EF=2
，DE=4
，DF=
， ∴AM=ME=
， ∵AM⊥ME， ∴∠AME=90°，
∴AE=
，
练习册系列答案
名校课堂系列答案
相关题目
