题目内容
 (2012•巴中)如图,四边形ABCD是平行四边形,以AB为直径的圆O经过点D,E是⊙O上一点,且∠AED=45°.
(2012•巴中)如图,四边形ABCD是平行四边形,以AB为直径的圆O经过点D,E是⊙O上一点,且∠AED=45°.(1)判断CD与⊙O的位置关系,并说明理由;
(2)若⊙O半径为6cm,AE=10cm,求∠ADE的正弦值.
分析:(1)首先连接OD,由在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可证得OD⊥AB,又由四边形ABCD是平行四边形,即可证得OD⊥CD,即可证得CD与⊙O相切;
(2)首先过点O作OF⊥AE,连接OE,由垂径定理可得AF=6cm,∠AOF=
∠AOE,又由圆周角定理可得∠ADE=
∠AOE,继而证得∠AOF=∠ADE,然后在Rt△AOF中,求得sin∠AOF的值,即可求得答案.
(2)首先过点O作OF⊥AE,连接OE,由垂径定理可得AF=6cm,∠AOF=
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:(1)CD与⊙O相切.
解:(1)CD与⊙O相切.
理由:连接OD,
∵∠AED=45°,
∴∠AOD=2∠AED=90°,
即OD⊥AB,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴OD⊥CD,
∵AB为直径的圆O经过点D,
∴CD与⊙O相切;
 (2)过点O作OF⊥AE,连接OE,
(2)过点O作OF⊥AE,连接OE,
则AF=
AE=
×10=5(cm),
∵OA=OE,
∴∠AOF=
∠AOE,
∵∠ADE=
∠AOE,
∴∠ADE=∠AOF,
在Rt△AOF中,sin∠AOF=
=
,
∴sin∠ADE=
.
 解:(1)CD与⊙O相切.
解:(1)CD与⊙O相切.理由:连接OD,
∵∠AED=45°,
∴∠AOD=2∠AED=90°,
即OD⊥AB,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴OD⊥CD,
∵AB为直径的圆O经过点D,
∴CD与⊙O相切;
 (2)过点O作OF⊥AE,连接OE,
(2)过点O作OF⊥AE,连接OE,则AF=
| 1 |
| 2 |
| 1 |
| 2 |
∵OA=OE,
∴∠AOF=
| 1 |
| 2 |
∵∠ADE=
| 1 |
| 2 |
∴∠ADE=∠AOF,
在Rt△AOF中,sin∠AOF=
| AF |
| AO |
| 5 |
| 6 |
∴sin∠ADE=
| 5 |
| 6 |
点评:此题考查了切线的判定、圆周角定理、垂径定理、平行四边形的性质以及三角函数等知识.此题综合性较强,难度适中,注意掌握辅助线的作法,注意数形结合思想与转化思想的应用.

练习册系列答案
相关题目
 点D与点A关于y轴对称,tan∠ACB=
点D与点A关于y轴对称,tan∠ACB=
 (2012•巴中)如图,已知AD是△ABC的BC边上的高,下列能使△ABD≌△ACD的条件是( )
(2012•巴中)如图,已知AD是△ABC的BC边上的高,下列能使△ABD≌△ACD的条件是( )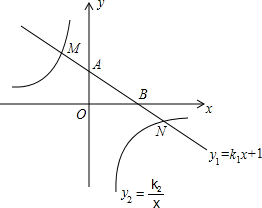 ,与x轴交于点B,与反比例函数y2=
,与x轴交于点B,与反比例函数y2= (2012•巴中)如图,点P是等边△ABC的边上的一个做匀速运动的动点,其由点A开始沿AB边运动到B再沿BC边运动到C为止,设运动时间为t,△ACP的面积为S,则S与t的大致图象是( )
(2012•巴中)如图,点P是等边△ABC的边上的一个做匀速运动的动点,其由点A开始沿AB边运动到B再沿BC边运动到C为止,设运动时间为t,△ACP的面积为S,则S与t的大致图象是( )