题目内容
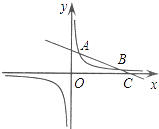
【题目】如图,已知函数![]() (x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(1)求△OCD的面积;
(2)当BE=![]() AC时,求CE的长.
AC时,求CE的长.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据函数![]() (x>0)的图象经过点A(1,2),求函数解析式,再有AC∥y轴,AC=1求出C点坐标,然后根据CD∥x轴,求D点坐标,从而可求CD长,最后利用三角形面积公式求出△OCD的面积.
(x>0)的图象经过点A(1,2),求函数解析式,再有AC∥y轴,AC=1求出C点坐标,然后根据CD∥x轴,求D点坐标,从而可求CD长,最后利用三角形面积公式求出△OCD的面积.
(2)通过BE=![]() AC,求得B点坐标,进而求得CE长.
AC,求得B点坐标,进而求得CE长.
试题解析:解:(1)∵函数![]() (x>0)的图象经过点A(1,2),
(x>0)的图象经过点A(1,2),
∴![]() ,即k=2.
,即k=2.
∵AC∥y轴,AC=1,∴点C的坐标为(1,1).
∵ CD∥x轴,点D在函数图像上,∴点D的坐标为(2,1).
∴![]() .
.
(2)∵BE=![]() AC,∴BE=
AC,∴BE=![]() .
.
∵BE⊥CD,∴点B的纵坐标是![]() .∴点B的横坐标是
.∴点B的横坐标是![]() .
.
∴CE=![]() .
.
考点:1.反比例函数综合题;3.曲线上点的坐标与方程的关系;3.三角形的面积.
【题型】解答题
【结束】
27
【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 均为整数),则有
均为整数),则有 ![]() .
.
∴![]() .这样小明就找到了一种把部分
.这样小明就找到了一种把部分![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当![]() 均为正整数时,若
均为正整数时,若![]() ,用含m、n的式子分别表示
,用含m、n的式子分别表示![]() ,得
,得 ![]() = ,
= ,![]() = ;
= ;
(2)利用所探索的结论,找一组正整数![]() ,填空: +
,填空: + ![]() =( +
=( + ![]() )2;
)2;
(3)若![]() ,且
,且![]() 均为正整数,求
均为正整数,求![]() 的值.
的值.
【答案】(1)![]() ;
;![]() ;(2)4,2,1,1(答案不唯一);(3)
;(2)4,2,1,1(答案不唯一);(3)![]() =7或13
=7或13
【解析】分析:(1)由a+b![]() =(m+n
=(m+n![]() )2,展开比较系数可得答案;
)2,展开比较系数可得答案;
(2)取m=1,n=1,可得a和b的值,可得答案;
(3)由题意得m和n的方程,解方程可得m和n,可得a值.
详解:(1)∵a+b![]() =(m+n
=(m+n![]() )2,
)2,
∴a+b![]() =m2+3n2+2mn
=m2+3n2+2mn![]() ,
,
∴a=m2+3n2,b=2mn.
故答案为:m2+3n2,2mn.
(2)设m=1,n=1,
∴a=m2+3n2=4,b=2mn=2.
故答案为4、2、1、1.
(3)由题意,得:
a=m2+3n2,b=2mn
∵4=2mn,且m、n为正整数,
∴m=2,n=1或者m=1,n=2,
∴a=22+3×12=7,或a=12+3×22=13.

【题目】城区某中学为形成体育特色,落实学生每天![]() 小时的锻炼时间,通过调查研究,决定在七、八、九年级分别开展跳绳、羽毛球、毽球的健身运动.
小时的锻炼时间,通过调查研究,决定在七、八、九年级分别开展跳绳、羽毛球、毽球的健身运动.
国家规定初中每班的标准人数为![]() 人,七年级共有八个班,各班人数情况如下表,八年级学生人数是七年级学生人数的
人,七年级共有八个班,各班人数情况如下表,八年级学生人数是七年级学生人数的![]() 倍少
倍少![]() 人,九年级学生人数的
人,九年级学生人数的![]() 倍刚好是七、八年级学生人数的总和.(注:
倍刚好是七、八年级学生人数的总和.(注:![]() 班表示七年级一班)
班表示七年级一班)
班级 |
|
|
|
|
|
|
|
|
和每班标准 人数的差值 |
|
|
|
|
|
|
|
|
![]() 用含
用含![]() 的式子表示该中学七年级学生总数;
的式子表示该中学七年级学生总数;
![]() 学校决定按每人一根跳绳、一个毽球,两人一副羽毛球拍的标准,购买相应的体育器材以满足学生锻炼需要,其中跳绳每根
学校决定按每人一根跳绳、一个毽球,两人一副羽毛球拍的标准,购买相应的体育器材以满足学生锻炼需要,其中跳绳每根![]() 元,毽球每个
元,毽球每个![]() 元,羽毛球拍每副
元,羽毛球拍每副![]() 元.请你计算当
元.请你计算当![]() 时,学校为落实
时,学校为落实![]() 小时体育锻炼时间需购买器材的费用是多少?
小时体育锻炼时间需购买器材的费用是多少?