题目内容
从边长为1的等边三角形内一点分别向三边作垂线，三条垂线段长的和为
- A.
- B.
- C.
- D.
A
分析：根据等积转换知：三条垂线段长的和等于等边三角形的高．运用三角函数求高即可．
解答：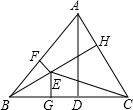
解：如图，EF⊥AB，EG⊥BC，EH⊥AC，AD为BC上的高，
则S△ABC=S△AEB+S△AEC+S△BEC，
∴
BC•AD=EG•BC+EH•AC+EF•AB=BC（EG+EH+EF），
∴AD=EG+EH+EF=ABsin∠ABC=ABsin60°=．
故选A．
点评：本题结合图形，利用锐角三角函数的概念和等边三角形的性质求解．等积转换是关键．
分析：根据等积转换知：三条垂线段长的和等于等边三角形的高．运用三角函数求高即可．
解答：
解：如图，EF⊥AB，EG⊥BC，EH⊥AC，AD为BC上的高，则S△ABC=S△AEB+S△AEC+S△BEC，
∴
BC•AD=EG•BC+EH•AC+EF•AB=BC（EG+EH+EF），∴AD=EG+EH+EF=ABsin∠ABC=ABsin60°=
．故选A．
点评：本题结合图形，利用锐角三角函数的概念和等边三角形的性质求解．等积转换是关键．
练习册系列答案
天天练口算系列答案
相关题目
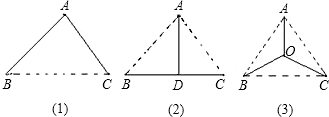
如图，动点O从边长为6的等边△ABC的顶点A出发，沿着ACBA的路线匀速运动一周，速度为1个单位长度每秒，以O为圆心、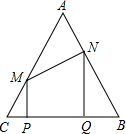
已知：如图，在边长为2的等边三角形△ABC中，点P以每秒1个单位从C向B运动，运动时间为t秒，且PQ=1，过P、Q点分别向BC作垂线，垂足分别为P、Q，交AC、AB于M、N，连接MN；