题目内容
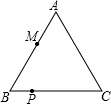 如图,△ABC是等边三角形,AB=6厘米,点P从点B出发,沿BC以每秒1厘米的速度运动到点C停止;同时点M从点B出发,沿折线BA-AC以每秒3厘米的速度运动到点C停止.如果其中一个点停止运动,则另一个点也停止运动.设点P的运动时间为t秒,P、M两点之间的距离为y厘米,则表示y与t的函数关系的图象大致是
如图,△ABC是等边三角形,AB=6厘米,点P从点B出发,沿BC以每秒1厘米的速度运动到点C停止;同时点M从点B出发,沿折线BA-AC以每秒3厘米的速度运动到点C停止.如果其中一个点停止运动,则另一个点也停止运动.设点P的运动时间为t秒,P、M两点之间的距离为y厘米,则表示y与t的函数关系的图象大致是
- A.
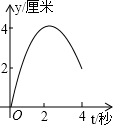
- B.

- C.
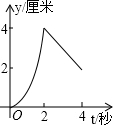
- D.
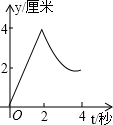
D
分析:分类讨论:当M点在AB上,作MD⊥BC于D,根据等边三角形性质得AB=BC=6,∠B=60°,则∠BMD=30°,利用含30度的直角三角形三边的关系可求出BD= t,MD=
t,MD= t,
t,
则PD= t,然后利用勾股定理可得到y=
t,然后利用勾股定理可得到y= t(0≤t≤2);当M点在AC上,作MD⊥BC于D,运用相同的方法可得到y=7t2-54t+108(2≤t≤4),利用二次函数的性质得t=-
t(0≤t≤2);当M点在AC上,作MD⊥BC于D,运用相同的方法可得到y=7t2-54t+108(2≤t≤4),利用二次函数的性质得t=-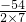 =
=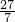 时,y有最小值,最后利用解析式对各选项中的图象进行判断即可得到答案.
时,y有最小值,最后利用解析式对各选项中的图象进行判断即可得到答案.
解答:当M点在AB上,作MD⊥BC于D,如图1,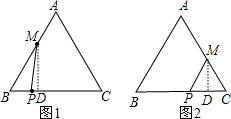
∵△ABC是等边三角形,
∴AB=BC=6,∠B=60°,
∴∠BMD=30°,
∵BM=3t,BP=t,
∴BD= BM=
BM= t,MD=
t,MD= BD=
BD= t,
t,
∴PD=BD-BP= t,
t,
在Rt△MPD中,PM2=MD2+PD2,即y2=( t)2+(
t)2+( t)2,
t)2,
∴y= t(0≤t≤2),
t(0≤t≤2),
当M点在AC上,作MD⊥BC于D,如图2,
∵△ABC是等边三角形,
∴AB=AC=6,∠C=60°,
∴∠CMD=30°,
∵BA+AMP=3t,BP=t,
∴CM=12-3t,
∴DC= MC=
MC= (12-3t),MD=
(12-3t),MD= DC=
DC= (12-3t),
(12-3t),
∴PD=BC-BP-CD= t,
t,
在Rt△MPD中,PM2=MD2+PD2,即y2=[ (12-3t)]2+(
(12-3t)]2+( t)2,
t)2,
∴y2=7t2-54t+108(2≤t≤4),
∴t=-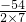 =
=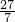 时,y有最小值,
时,y有最小值,
综上所述当0≤t≤2时,y与t的函数关系的图象为以原点为端点的线段;当2≤t≤4时,y与t的函数关系的图象为开口向上的抛物线的一部分,且t=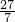 时,y有最小值.
时,y有最小值.
故选D.
点评:本题考查了动点问题的函数图象:利用点运动的几何性质列出有关的函数关系式,然后根据函数关系式画出函数图象,注意自变量的取值范围;重点考查了通过看图获取信息,解决生活中的实际问题.
分析:分类讨论:当M点在AB上,作MD⊥BC于D,根据等边三角形性质得AB=BC=6,∠B=60°,则∠BMD=30°,利用含30度的直角三角形三边的关系可求出BD=
 t,MD=
t,MD= t,
t,则PD=
 t,然后利用勾股定理可得到y=
t,然后利用勾股定理可得到y= t(0≤t≤2);当M点在AC上,作MD⊥BC于D,运用相同的方法可得到y=7t2-54t+108(2≤t≤4),利用二次函数的性质得t=-
t(0≤t≤2);当M点在AC上,作MD⊥BC于D,运用相同的方法可得到y=7t2-54t+108(2≤t≤4),利用二次函数的性质得t=-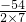 =
=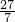 时,y有最小值,最后利用解析式对各选项中的图象进行判断即可得到答案.
时,y有最小值,最后利用解析式对各选项中的图象进行判断即可得到答案.解答:当M点在AB上,作MD⊥BC于D,如图1,

∵△ABC是等边三角形,
∴AB=BC=6,∠B=60°,
∴∠BMD=30°,
∵BM=3t,BP=t,
∴BD=
 BM=
BM= t,MD=
t,MD= BD=
BD= t,
t,∴PD=BD-BP=
 t,
t,在Rt△MPD中,PM2=MD2+PD2,即y2=(
 t)2+(
t)2+( t)2,
t)2,∴y=
 t(0≤t≤2),
t(0≤t≤2),当M点在AC上,作MD⊥BC于D,如图2,
∵△ABC是等边三角形,
∴AB=AC=6,∠C=60°,
∴∠CMD=30°,
∵BA+AMP=3t,BP=t,
∴CM=12-3t,
∴DC=
 MC=
MC= (12-3t),MD=
(12-3t),MD= DC=
DC= (12-3t),
(12-3t),∴PD=BC-BP-CD=
 t,
t,在Rt△MPD中,PM2=MD2+PD2,即y2=[
 (12-3t)]2+(
(12-3t)]2+( t)2,
t)2,∴y2=7t2-54t+108(2≤t≤4),
∴t=-
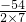 =
=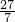 时,y有最小值,
时,y有最小值,综上所述当0≤t≤2时,y与t的函数关系的图象为以原点为端点的线段;当2≤t≤4时,y与t的函数关系的图象为开口向上的抛物线的一部分,且t=
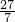 时,y有最小值.
时,y有最小值.故选D.
点评:本题考查了动点问题的函数图象:利用点运动的几何性质列出有关的函数关系式,然后根据函数关系式画出函数图象,注意自变量的取值范围;重点考查了通过看图获取信息,解决生活中的实际问题.

练习册系列答案
相关题目
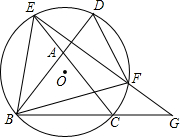 ∥AC,EF的延长线交BC的延长线于点G.
∥AC,EF的延长线交BC的延长线于点G. 9、如图,△ABC是等边三角形,过AB边上一点D作BC的平行线交AC于E,则△ADE的三个内角
9、如图,△ABC是等边三角形,过AB边上一点D作BC的平行线交AC于E,则△ADE的三个内角 如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于
如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于 如图,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,将△ABD绕点A点逆时针方向旋转后到达△ACE的位置,那么旋转角的度数是
如图,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,将△ABD绕点A点逆时针方向旋转后到达△ACE的位置,那么旋转角的度数是 如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.