题目内容
若关于x的一元二次方程(k-1)x2-(2k+1)x+k=0有两个不相等的实数根,则k的取值范围是
- A.

- B.
 且k≠1
且k≠1 - C.

- D.k≥
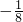 且k≠0
且k≠0
B
分析:一元二次方程(k-1)x2-(2k+1)x+k=0有两个不相等的实数根的条件是:①二次项系数不等于0;②根的判别式△=b2-4ac>0.
解答:∵关于x的一元二次方程(k-1)x2-(2k+1)x+k=0有两个不相等的实数根,
∴△=[-(2k+1)]2-4(k-1)•k=8k+1>0,
即8k+1>0,解得k>- ;
;
又∵k-1≠0,
∴k的取值范围是:k>- 且k≠1.
且k≠1.
故选B.
点评:本题考查了一元二次方程的根的判别式.一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
分析:一元二次方程(k-1)x2-(2k+1)x+k=0有两个不相等的实数根的条件是:①二次项系数不等于0;②根的判别式△=b2-4ac>0.
解答:∵关于x的一元二次方程(k-1)x2-(2k+1)x+k=0有两个不相等的实数根,
∴△=[-(2k+1)]2-4(k-1)•k=8k+1>0,
即8k+1>0,解得k>-
 ;
;又∵k-1≠0,
∴k的取值范围是:k>-
 且k≠1.
且k≠1.故选B.
点评:本题考查了一元二次方程的根的判别式.一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目