题目内容
如图,抛物线y=ax2-2ax+c的图象与x轴交于A、B(3,0),与y轴交于C(0,- )
)
(1)求二次函数解析式;
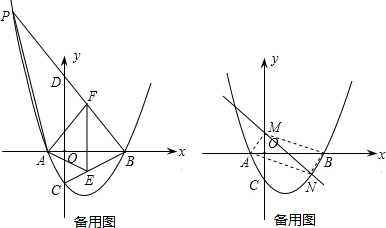
(2)P为第二象限抛物线上一点,且∠PBA=∠OCB,点E在线段CB上,过E作x轴的垂线交PB于F,当△AEF面积最大时,求点E坐标;
(3)设直线l:y=kx+b交y轴于M,交抛物线于N,若A、M、N、B为顶点的四边形为平行四边形,求直线l解析式.

解:(1)∵抛物线y=ax2-2ax+c的图象经过B(3,0),C(0,- ),
),
∴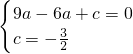 ,
,
解得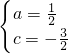 ,
,
所以,抛物线解析式为y= x2-x-
x2-x- ;
;
(2)如图,设直线PB与y轴相交于点D,
∵B(3,0),C(0,- ),
),
∴OC= ,OB=3,
,OB=3,
∵∠PBA=∠OCB,∠BOC=∠BOD=90°,
∴△BOC∽△DOB,
∴ =
= ,
,
即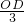 =
=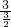 ,
,
解得OD=6,
∴点D的坐标为(0,6),
设直线PB的解析式为y=ex+f,直线BC的解析式为y=mx+n,
则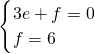 ,
,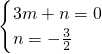 ,
,
解得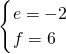 ,
, ,
,
所以,直线PB的解析式为y=-2x+6,直线BC的解析式为y= x-
x- ,
,
令y=0,则 x2-x-
x2-x- =0,
=0,
解得x1=3,x2=-1,
所以,点A的坐标为(-1,0),
设点E的横坐标为x,则点E(x, x-
x- ),F(x,-2x+6),
),F(x,-2x+6),
EF=-2x+6- x+
x+ =-
=- x+
x+ ,
,
点A到EF的距离为x-(-1)=x+1,
S△AEF= ×(-
×(- x+
x+ )×(x+1),
)×(x+1),
=- (x-3)(x+1),
(x-3)(x+1),
=- (x2-2x-3),
(x2-2x-3),
=- (x-1)2+5,
(x-1)2+5,
所以,当x=1时,△AEF面积最大,
此时 ×1-
×1- =-1,
=-1,
所以,点E的坐标为(1,-1);
(3)∵A(-1,0),B(3,0),
∴AB=3-(-1)=3+1=4,
①AB是平行四边形的边时,直线l与x轴平行,
此时k=0,MN=AB=4,
所以,点N的横坐标为4或-4,
当点N的横坐标为4时,y= ×42-4-
×42-4- =
= ,
,
此时,直线l的解析式为y= ,
,
当点N的横坐标为-4时,y= ×(-4)2-(-4)-
×(-4)2-(-4)- =
= ,
,
此时,直线l的解析式为y= ,
,
②AB是平行四边形的对角线时,根据平行四边形的对角线互相平分,
∵A(-1,0),B(3,0),
∴平行四边形的中心坐标为(1,0),
∵点M在y轴上,
∴点N的横坐标为2,
此时,y= ×22-2-
×22-2- =-
=- ,
,
∴点N的坐标为(2,- ),
),
∴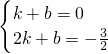 ,
,
解得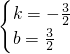 ,
,
所以,直线l的解析式为y=- x+
x+ ,
,
综上所述,直线l的解析式为:y= 或y=
或y= 或y=-
或y=- x+
x+ .
.
分析:(1)把点B、C的坐标代入抛物线解析式,利用待定系数法求函数解析式解答;
(2)设PB与y轴相交于点D,根据点B、C的坐标求出OC、OB的长度,然后利用相似三角形对应边成比例求出OD的长度,从而得到点D的坐标,再利用待定系数法求直线解析式求出直线PB的解析式与直线BC的解析式,设点E的横坐标为x,根据两直线的解析式表示出E、F的坐标,再根据抛物线解析式求出点A的坐标,然后表示出EF的长度与点A到EF的距离,然后根据三角形的面积公式列式整理,再根据二次函数的最值问题解答得到x的值,便不难求出点E的坐标;
(3)先根据AB的坐标求出AB的长度,再分①AB是平行四边形的边时,直线l与x轴平行,根据平行四边形对边相等求出MN的长度,然后分点N在第一象限与第二象限得到点N的横坐标,再代入抛物线解析式计算求出纵坐标,从而得解;②AB是平行四边形的对角线时,根据平行四边形的对角线互相平分求出平行四边形的中心坐标是(1,0),然后求出点N的横坐标是2,代入抛物线解析式求出点N的纵坐标,再利用待定系数法求直线解析式计算即可得解.
点评:本题是对二次函数的综合考查,主要利用了待定系数法求函数解析式,相似三角形对应边成比例,三角形的面积,二次函数的最值问题,平行四边形的对边平行且相等,对角线互相平分的性质,(3)要注意AB为平行四边形的边时,直线l与x轴平行的情况的讨论.
 ),
),∴
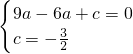 ,
,解得
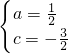 ,
,所以,抛物线解析式为y=
 x2-x-
x2-x- ;
;(2)如图,设直线PB与y轴相交于点D,
∵B(3,0),C(0,-
 ),
),∴OC=
 ,OB=3,
,OB=3,∵∠PBA=∠OCB,∠BOC=∠BOD=90°,
∴△BOC∽△DOB,
∴
 =
= ,
,即
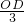 =
=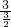 ,
,解得OD=6,
∴点D的坐标为(0,6),
设直线PB的解析式为y=ex+f,直线BC的解析式为y=mx+n,
则
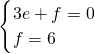 ,
,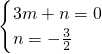 ,
,解得
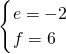 ,
, ,
,
所以,直线PB的解析式为y=-2x+6,直线BC的解析式为y=
 x-
x- ,
,令y=0,则
 x2-x-
x2-x- =0,
=0,解得x1=3,x2=-1,
所以,点A的坐标为(-1,0),
设点E的横坐标为x,则点E(x,
 x-
x- ),F(x,-2x+6),
),F(x,-2x+6),EF=-2x+6-
 x+
x+ =-
=- x+
x+ ,
,点A到EF的距离为x-(-1)=x+1,
S△AEF=
 ×(-
×(- x+
x+ )×(x+1),
)×(x+1),=-
 (x-3)(x+1),
(x-3)(x+1),=-
 (x2-2x-3),
(x2-2x-3),=-
 (x-1)2+5,
(x-1)2+5,所以,当x=1时,△AEF面积最大,
此时
 ×1-
×1- =-1,
=-1,所以,点E的坐标为(1,-1);
(3)∵A(-1,0),B(3,0),
∴AB=3-(-1)=3+1=4,
①AB是平行四边形的边时,直线l与x轴平行,
此时k=0,MN=AB=4,
所以,点N的横坐标为4或-4,
当点N的横坐标为4时,y=
 ×42-4-
×42-4- =
= ,
,此时,直线l的解析式为y=
 ,
,当点N的横坐标为-4时,y=
 ×(-4)2-(-4)-
×(-4)2-(-4)- =
= ,
,此时,直线l的解析式为y=
 ,
,②AB是平行四边形的对角线时,根据平行四边形的对角线互相平分,
∵A(-1,0),B(3,0),
∴平行四边形的中心坐标为(1,0),
∵点M在y轴上,
∴点N的横坐标为2,
此时,y=
 ×22-2-
×22-2- =-
=- ,
,∴点N的坐标为(2,-
 ),
),∴
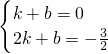 ,
,解得
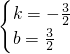 ,
,所以,直线l的解析式为y=-
 x+
x+ ,
,综上所述,直线l的解析式为:y=
 或y=
或y= 或y=-
或y=- x+
x+ .
.分析:(1)把点B、C的坐标代入抛物线解析式,利用待定系数法求函数解析式解答;
(2)设PB与y轴相交于点D,根据点B、C的坐标求出OC、OB的长度,然后利用相似三角形对应边成比例求出OD的长度,从而得到点D的坐标,再利用待定系数法求直线解析式求出直线PB的解析式与直线BC的解析式,设点E的横坐标为x,根据两直线的解析式表示出E、F的坐标,再根据抛物线解析式求出点A的坐标,然后表示出EF的长度与点A到EF的距离,然后根据三角形的面积公式列式整理,再根据二次函数的最值问题解答得到x的值,便不难求出点E的坐标;
(3)先根据AB的坐标求出AB的长度,再分①AB是平行四边形的边时,直线l与x轴平行,根据平行四边形对边相等求出MN的长度,然后分点N在第一象限与第二象限得到点N的横坐标,再代入抛物线解析式计算求出纵坐标,从而得解;②AB是平行四边形的对角线时,根据平行四边形的对角线互相平分求出平行四边形的中心坐标是(1,0),然后求出点N的横坐标是2,代入抛物线解析式求出点N的纵坐标,再利用待定系数法求直线解析式计算即可得解.
点评:本题是对二次函数的综合考查,主要利用了待定系数法求函数解析式,相似三角形对应边成比例,三角形的面积,二次函数的最值问题,平行四边形的对边平行且相等,对角线互相平分的性质,(3)要注意AB为平行四边形的边时,直线l与x轴平行的情况的讨论.

练习册系列答案
相关题目
 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少? O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).