ћвƒњƒЏ»Ё
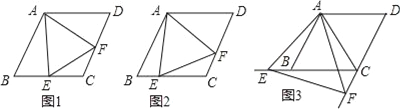
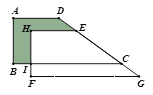
°Њћвƒњ°њ»зЌЉ1£ђ‘ЏRt°чABC÷–£ђ°ѕC=90°г£ђAC=6£ђBC=8£ђґѓµгPі”µгAњ™ Љ—Ў±яACѕтµгC“‘1Єцµ•ќї≥§ґ»µƒЋўґ»‘Ћґѓ£ђґѓµгQі”µгCњ™ Љ—Ў±яCBѕтµгB“‘√њ√л2Єцµ•ќї≥§ґ»µƒЋўґ»‘Ћґѓ£ђєэµгP„чPD//BC£ђљїAB”ЏµгD£ђЅђљ”PQЈ÷±рі”µгA°ҐCЌђ ±≥цЈҐ£ђµ±∆д÷–“їµгµљіпґЋµг ±£ђЅн“їµг“≤Ћж÷ЃЌ£÷є‘Ћґѓ£ђ…и‘Ћґѓ ±Љдќ™t√л£®t°Ё0£©£Ѓ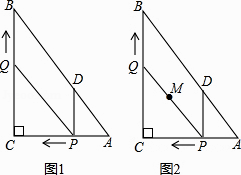
£®1£©÷±љ””√Їђtµƒіъ э љЈ÷±р±н Њ£ЇQB= £ђ PD= £Ѓ
£®2£© «Јсіж‘Џtµƒ÷µ£ђ єЋƒ±я–ќPDBQќ™Ѕв–ќ£њ»фіж‘Џ£ђ«у≥цtµƒ÷µ£ї»ф≤їіж‘Џ£ђЋµ√чјн”…£Ѓ≤ҐћљЊњ»зЇќЄƒ±дQµƒЋўґ»£®‘»Ћў‘Ћґѓ£©£ђ єЋƒ±я–ќPDBQ‘Џƒ≥“ї ±њћќ™Ѕв–ќ£ђ«уµгQµƒЋўґ»£ї
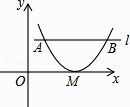
£®3£©»зЌЉ2£ђ‘Џ’ыЄц‘Ћґѓєэ≥ћ÷–£ђ«у≥цѕяґќPQ÷–µгMЋщЊ≠єэµƒ¬ЈЊґ≥§£Ѓ
°Њір∞Є°њ
£®1£©8©Б2t£ї![]()
t
£®2£©
љв£Ї≤їіж‘Џ
‘ЏRt°чABC÷–£ђ°ѕC=90°г£ђAC=6£ђBC=8£ђ
°аAB=10
°яPD//BC£ђ
°а°чAPD°„°чACB£ђ
°а ![]() £ђЉі
£ђЉі ![]() £ђ
£ђ
°аAD= ![]() t£ђ
t£ђ
°аBD=AB©БAD=10©Б ![]() t£ђ
t£ђ
°яBQ//DP£ђ
°аµ±BQ=DP ±£ђЋƒ±я–ќPDBQ «∆љ––Ћƒ±я–ќ£ђ
Љі8©Б2t= ![]() £ђљвµ√£Їt=
£ђљвµ√£Їt= ![]() £Ѓ
£Ѓ
µ±t= ![]() ±£ђPD=
±£ђPD= ![]() =
= ![]() £ђBD=10©Б
£ђBD=10©Б ![]() °Ѕ
°Ѕ ![]() =6£ђ
=6£ђ
°аDP°ўBD£ђ
°аPDBQ≤їƒ№ќ™Ѕв–ќ£Ѓ
…иµгQµƒЋўґ»ќ™√њ√лvЄцµ•ќї≥§ґ»£ђ
‘тBQ=8©Бvt£ђPD= ![]() t£ђBD=10©Б
t£ђBD=10©Б ![]() t£ђ
t£ђ
“™ єЋƒ±я–ќPDBQќ™Ѕв–ќ£ђ‘тPD=BD=BQ£ђ
µ±PD=BD ±£ђЉі ![]() t=10©Б
t=10©Б ![]() t£ђљвµ√£Їt=
t£ђљвµ√£Їt= ![]()
µ±PD=BQ£ђt= ![]() ±£ђЉі
±£ђЉі ![]() =8©Б
=8©Б ![]() £ђљвµ√£Їv=
£ђљвµ√£Їv= ![]()
µ±µгQµƒЋўґ»ќ™√њ√л ![]() Єцµ•ќї≥§ґ» ±£ђЊ≠єэ
Єцµ•ќї≥§ґ» ±£ђЊ≠єэ ![]() √л£ђЋƒ±я–ќPDBQ «Ѕв–ќ
√л£ђЋƒ±я–ќPDBQ «Ѕв–ќ
£®3£©
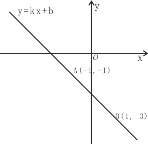
љв£Ї»зЌЉ2£ђ“‘Cќ™‘≠µг£ђ“‘ACЋщ‘Џµƒ÷±ѕяќ™x÷б£ђљ®ЅҐ∆љ√ж÷±љ«„ш±кѕµ£Ѓ
“јћв“в£ђњ…÷™0°№t°№4£ђµ±t=0 ±£ђµгM1µƒ„ш±кќ™£®3£ђ0£©£ђµ±t=4 ±µгM2µƒ„ш±кќ™£®1£ђ4£©£Ѓ
…и÷±ѕяM1M2µƒљвќц љќ™y=kx+b£ђ
°а ![]() £ђ
£ђ
љвµ√ ![]() £ђ
£ђ
°а÷±ѕяM1M2µƒљвќц љќ™y=©Б2x+6£Ѓ
°яµгQ£®0£ђ2t£©£ђP£®6©Бt£ђ0£©
°а‘Џ‘Ћґѓєэ≥ћ÷–£ђѕяґќPQ÷–µгM3µƒ„ш±к£® ![]() £ђt£©£Ѓ
£ђt£©£Ѓ
∞—x= ![]() іъ»лy=©Б2x+6µ√y=©Б2°Ѕ
іъ»лy=©Б2x+6µ√y=©Б2°Ѕ ![]() +6=t£ђ
+6=t£ђ
°аµгM3‘Џ÷±ѕяM1M2…ѕ£Ѓ
єэµгM2„чM2N°Ќx÷б”ЏµгN£ђ‘тM2N=4£ђM1N=2£Ѓ
°аM1M2=2 ![]()
°аѕяґќPQ÷–µгMЋщЊ≠єэµƒ¬ЈЊґ≥§ќ™2 ![]() µ•ќї≥§ґ»£Ѓ
µ•ќї≥§ґ»£Ѓ
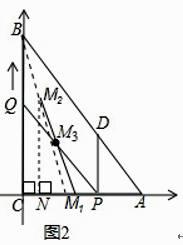
°Њљвќц°њљв£Ї£®1£©ЄщЊЁћв“вµ√£ЇCQ=2t£ђPA=t£ђ
°аQB=8©Б2t£ђ
°я‘ЏRt°чABC÷–£ђ°ѕC=90°г£ђAC=6£ђBC=8£ђPD//BC£ђ
°а°ѕAPD=90°г£ђ
°аtanA= ![]() =
= ![]() £ђ
£ђ
°аPD= ![]() t£Ѓ
t£Ѓ
Ћщ“‘ір∞Є «£Ї£®1£©8©Б2t£ђ ![]() t£Ѓ
t£Ѓ
°ЊњЉµгЊЂќц°њ±Њћв÷ч“™њЉ≤йЅЋЅв–ќµƒ–‘÷ ЇЌѕаЋ∆»эљ«–ќµƒ”¶”√µƒѕаєЎ÷™ ґµг£ђ–и“™’∆ќ’Ѕв–ќµƒЋƒћх±яґЉѕаµ»£їЅв–ќµƒґ‘љ«ѕяї•ѕаіє÷±£ђ≤Ґ«“√њ“їћхґ‘љ«ѕя∆љЈ÷“ї„йґ‘љ«£їЅв–ќ±їЅљћхґ‘љ«ѕяЈ÷≥…ЋƒЄц»Ђµ»µƒ÷±љ«»эљ«–ќ£їЅв–ќµƒ√жїэµ»”ЏЅљћхґ‘љ«ѕя≥§µƒїэµƒ“ї∞л£ї≤вЄя£Ї≤вЅњ≤їƒ№µљіпґ•≤њµƒќпћеµƒЄяґ»£ђЌ®≥£”√°∞‘ЏЌђ“ї ±њћќпЄя”л”∞≥§≥…±»јэ°±µƒ‘≠јнљвЊц£ї≤вЊа£Ї≤вЅњ≤їƒ№µљіпЅљµгЉдµƒЊўјэ£ђ≥£єє‘мѕаЋ∆»эљ«–ќ«уљв≤≈ƒ№’э»ЈљвіріЋћв£Ѓ