题目内容
如图,在矩形ABCD中,O是AC与BD的交点,过O点的直线EF与AB、CD的延长线分别交于E、F.
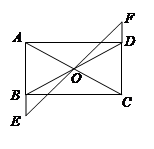
(1)求证:△BOE≌△DOF;
(2)当EF与AC满足____▲_____关系时,以A、E、C、F为顶点的四边形是菱形.
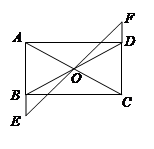
(1)求证:△BOE≌△DOF;
(2)当EF与AC满足____▲_____关系时,以A、E、C、F为顶点的四边形是菱形.
(1)见解析(2)EF⊥AC
(1)证明:∵四边形ABCD是矩形,
∴OB=OD(矩形的对角线互相平分),
AE∥CF(矩形的对边平行).
∴∠E=∠F,∠OBE=∠ODF.
∴△BOE≌△DOF(AAS).(4分)
(2)解:当EF⊥AC时,四边形AECF是菱形.(5分)
证明:∵四边形ABCD是矩形,
∴OA=OC(矩形的对角线互相平分).
又由(1)△BOE≌△DOF得,
OE=OF,
∴四边形AECF是平行四边形(对角线互相平分的四边形是平行四边形)(6分)
又EF⊥AC,
∴四边形AECF是菱形(对角线互相垂直的平行四边形是菱形).(8分)
(1)由矩形的性质:OB=OD,AE∥CF证得△BOE≌△DOF;
(2)根据对角线互相垂直平分的四边形是菱形求证
∴OB=OD(矩形的对角线互相平分),
AE∥CF(矩形的对边平行).
∴∠E=∠F,∠OBE=∠ODF.
∴△BOE≌△DOF(AAS).(4分)
(2)解:当EF⊥AC时,四边形AECF是菱形.(5分)
证明:∵四边形ABCD是矩形,
∴OA=OC(矩形的对角线互相平分).
又由(1)△BOE≌△DOF得,
OE=OF,
∴四边形AECF是平行四边形(对角线互相平分的四边形是平行四边形)(6分)
又EF⊥AC,
∴四边形AECF是菱形(对角线互相垂直的平行四边形是菱形).(8分)
(1)由矩形的性质:OB=OD,AE∥CF证得△BOE≌△DOF;
(2)根据对角线互相垂直平分的四边形是菱形求证

练习册系列答案
相关题目

 中,
中, 且
且 ,
, 、
、 分别是两底的中点,连结
分别是两底的中点,连结 ,若
,若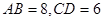 ,求
,求





