题目内容
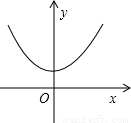
若记函数y在x处的值为f(x),(例如y=x2,也可记着f(x)=x2)已知函数f(x)=ax2+bx+c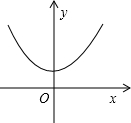 的图象如图所示,且ax2+(b-1)x+c>0对所有的实数x都成立,则下列结论成立的有
的图象如图所示,且ax2+(b-1)x+c>0对所有的实数x都成立,则下列结论成立的有(1)ac>0,
(2)
| (b-1)2 | 4 |
(3)对所有的实数x都有f(x)>x,
(4)对所有的实数x都有f(f(x))>x.
分析:(1)抛物线开口向上,则a>0,抛物线与y轴的交点在x轴上方,则c>0,可判断(1)正确;
(2)根据ax2+(b-1)x+c>0对所有的实数x都成立,可得到抛物线与x轴没有交点,则△<0,变形△<0即可对(2)进行判断;
(3)把ax2+(b-1)x+c>0进行变形即可得到ax2+bx+c>x;
(4)把f(x)作为变量得到f(f(x))>f(x),即有(4)的结论.
(2)根据ax2+(b-1)x+c>0对所有的实数x都成立,可得到抛物线与x轴没有交点,则△<0,变形△<0即可对(2)进行判断;
(3)把ax2+(b-1)x+c>0进行变形即可得到ax2+bx+c>x;
(4)把f(x)作为变量得到f(f(x))>f(x),即有(4)的结论.
解答:解:(1)观察图象得,a>0,c>0,则ac>0,所以(1)正确;
(2)∵ax2+(b-1)x+c>0对所有的实数x都成立,且a>0,
∴y=ax2+(b-1)x+c的图象在x轴上方,
∴△<0,即(b-1)2-4ac<0,
∴
<ac,所以(2)正确;
(3)∵ax2+(b-1)x+c>0对所有的实数x都成立,
∴ax2+bx+c>x对所有的实数x都成立,
即对所有的实数x都有f(x)>x,所以(3)正确;
(4)由(3)得对所有的实数x都有f(x)>x,
∴f(f(x))>f(x),
∴对所有的实数x都有f(f(x))>x.
故答案为(1)、(2)、(3)、(4).
(2)∵ax2+(b-1)x+c>0对所有的实数x都成立,且a>0,
∴y=ax2+(b-1)x+c的图象在x轴上方,
∴△<0,即(b-1)2-4ac<0,
∴
| (b-1)2 |
| 4 |
(3)∵ax2+(b-1)x+c>0对所有的实数x都成立,
∴ax2+bx+c>x对所有的实数x都成立,
即对所有的实数x都有f(x)>x,所以(3)正确;
(4)由(3)得对所有的实数x都有f(x)>x,
∴f(f(x))>f(x),
∴对所有的实数x都有f(f(x))>x.
故答案为(1)、(2)、(3)、(4).
点评:本题考查了二次函数ax2+bx+c=0(a≠0)的有关性质:a>0,开口向上;a<0,开口向下;c>0,抛物线与y轴的交点在x轴上方;c=0,过原点;c<0,抛物线与y轴的交点在x轴下方;△>0,抛物线与x轴有两个交点;△=0,抛物线与x轴有一个公共点;△<0,抛物线与x轴没有个公共点.也考查了代数式的变形能力.

练习册系列答案
相关题目
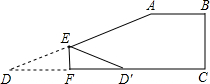 如图,直角梯形纸片ABCD,AB∥CD,∠B=90°,AB=BC=2cm,tan∠D=
如图,直角梯形纸片ABCD,AB∥CD,∠B=90°,AB=BC=2cm,tan∠D= 的图象如图所示,且ax2+(b-1)x+c>0对所有的实数x都成立,则下列结论成立的有______.
的图象如图所示,且ax2+(b-1)x+c>0对所有的实数x都成立,则下列结论成立的有______.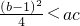 ,
,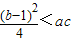 ,
,