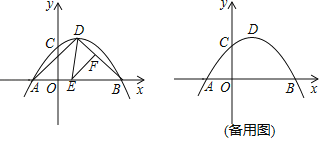题目内容
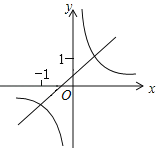
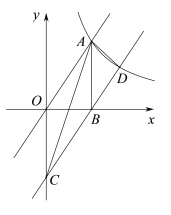
【题目】如图,正比例函数y1=kx与反比例函数![]() (x>0)交于点A(2,3),AB⊥x轴于点B,平移直线y1=kx使其经过点B,得到直线y2,y2与y轴交于点C,与
(x>0)交于点A(2,3),AB⊥x轴于点B,平移直线y1=kx使其经过点B,得到直线y2,y2与y轴交于点C,与![]() 交于点D.
交于点D.
(1)求正比例函数y1=kx及反比例函数![]() 的解析式;
的解析式;
(2)求点D的坐标;
(3)求△ACD的面积.
【答案】(1)y1=![]() x,
x,![]() ;(2)D坐标为(
;(2)D坐标为(![]() ,
,![]() );(3)
);(3)![]() .
.
【解析】
(1)用待定系数法,即可求得;(2)y2由y1平移得到,所以设y2=![]() x+b,然后通过点B求出平移后的函数解析式,然后与
x+b,然后通过点B求出平移后的函数解析式,然后与![]() 联立,即可确定D的坐标;(3)通过D点坐标确定DE的长,用S△ACD=S△OCD面积相等,法求出OC的长,计算即可.
联立,即可确定D的坐标;(3)通过D点坐标确定DE的长,用S△ACD=S△OCD面积相等,法求出OC的长,计算即可.
解:(1)将点A(2,3)分别带入y1=kx、![]() 得3=2k、
得3=2k、![]() ,解得k=
,解得k=![]() ,m=6,
,m=6,
∴正比例函数y1=kx及反比例函数![]() 的解析式分别为y1=
的解析式分别为y1=![]() x、
x、![]() ;
;
(2)∵y2由y1平移得到,所以设y2=![]() x+b,
x+b,
∵AB⊥x轴,
∴B(2,0),将其带入y2=![]() x+b得b=-3,
x+b得b=-3,
∴y2=![]() x-3,
x-3,
解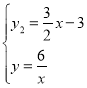 得
得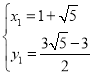 ,
,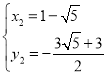 (舍),
(舍),
∴点D坐标为(![]() ,
,![]() );
);
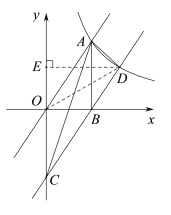
(3)如答图,连接OD,作DE⊥y轴于E,则DE=![]() ,
,
∵直线y1∥y2,
∴S△ACD=S△OCD=![]() ×OC×DE=
×OC×DE=![]() ×3×(
×3×(![]() )=
)=![]() .
.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目