题目内容
【题目】如图1，在平面直角坐标系中，直线AB与x轴、y轴相交于
、
两点，动点C在线段OA上（不与O、A重合），将线段CB绕着点C顺时针旋转
得到CD，当点D恰好落在直线AB上时，过点D作
轴于点E.
（1）求证，
；
（2）如图2，将
沿x轴正方向平移得
，当直线
经过点D时，求点D的坐标及平移的距离；
（3）若点P在y轴上，点Q在直线AB上，是否存在以C、D、P、Q为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的Q点坐标，若不存在，请说明理由.
【答案】（1）
，见解析；（2）D（3，1），
平移的距离是
个单位，见解析；（3）存在满足条件的点Q，其坐标为
或
或
，见解析.
【解析】
（1）根据AAS或ASA即可证明；
（2）首先求直线AB的解析式，再求出出点D的坐标，再求出直线B′C′的解析式，求出点C′的坐标即可解决问题；
（3）如图3中，作CP∥AB交y轴于P，作PQ∥CD交AB于Q，则四边形PCDQ是平行四边形，求出直线PC的解析式，可得点P坐标，点C向左平移1个单位，向上平移
个单位得到P，推出点D向左平移1个单位，向上平移个单位得到Q，再根据对称性可得Q′、Q″的坐标.
（1）∵
，
∴
，
，
∴
，
∵
，
∴
（2）∵直线AB与x轴，y轴交于
、
两点
∴直线AB的解析式为
∵，
∴
，设
，则
把代入得到
，
∴
∵，
∴直线BC的解析式为
，
设直线
的解析式为
，把代入得到
∴直线的解析式为
，
∴
，
∴
∴平移的距离是个单位.
（3）如图3中，作CP∥AB交y轴于P，作PQ∥CD交AB于Q，则四边形PCDQ是平行四边形，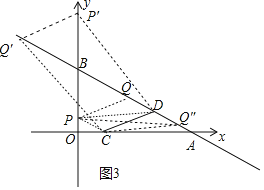
易知直线PC的解析式为y=-
x+
，
∴P（0，），
∵点C向左平移1个单位，向上平移个单位得到P，
∴点D向左平移1个单位，向上平移个单位得到Q，
∴Q（2，
），
当CD为对角线时，四边形PCQ″D是平行四边形，可得Q″，
当四边形CDP′Q′为平行四边形时，可得Q′，
综上所述， 存在满足条件的点Q，其坐标为
或或
