题目内容
1. 如图,⊙O的半径为5,AB为弦,半径OC⊥AB,垂足为点E,若OE=3,则AB的长是( )
如图,⊙O的半径为5,AB为弦,半径OC⊥AB,垂足为点E,若OE=3,则AB的长是( )| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
分析 连接OA,根据勾股定理求出AE的长,进而可得出结论.
解答  解:连接OA,
解:连接OA,
∵OC⊥AB,OA=5,OE=3,
∴AE=$\sqrt{{OA}^{2}-{OE}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴AB=2AE=8.
故选C.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
13.已知△ABC,过点C作CD⊥AB,交AB于D,如果$\frac{AC}{BC}=\frac{AD}{CD}$,那么△ABC是( )
| A. | 锐角三角形 | B. | 等腰三角形 | C. | 直角三角形 | D. | 等边三角形 |
11.如表有六张卡片,卡片正面分别写有六个数字,背面分别写有六个字母.
将卡片正面的数由大到小排列,然后将卡片翻转,卡片上的字母组成的单词是thanks.
| 正面 | -(-1) | |-2| | (-1)3 | 0 | -3 | +5 |
| 背面 | a | h | k | n | s | t |
 如图,已知AC=AD,BC=BD,△ABC和△ABD全等吗?并说明你的理由.
如图,已知AC=AD,BC=BD,△ABC和△ABD全等吗?并说明你的理由.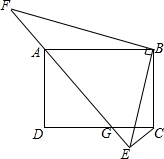 如图,在矩形ABCD中,AB=4,BC=3,G是CD边上的动点(点G不与点C、D重合),CE⊥AG的延长线于G点,BF⊥BE交EA的延长线于F点.
如图,在矩形ABCD中,AB=4,BC=3,G是CD边上的动点(点G不与点C、D重合),CE⊥AG的延长线于G点,BF⊥BE交EA的延长线于F点.