Question

【题目】如图，在△ABC中，AB=AC，且点A的坐标为（﹣3，0），点C坐标为（0， ），点B在y轴的负半轴上，抛物线y=﹣ x2+bx+c经过点A和点C

（1）求b，c的值；
（2）在抛物线的对称轴上是否存在点Q，使得△ACQ为等腰三角形？若存在，直接写出点Q的坐标；若不存在，请说明理由
（3）点P是线段AO上的一个动点，过点P作y轴的平行线交抛物线于点M，交AB于点E，探究：当点P在什么位置时，四边形MEBC是平行四边形，此时，请判断四边形AECM的形状，并说明理由．

Answer 1

【答案】
（1）

解：∵点A的坐标为（﹣3，0），点C坐标为（0， ），点B在y轴的负半轴上，抛物线y=﹣ x2+bx+c经过点A和点C，

∴ ，

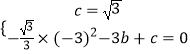解得： ；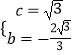

（2）

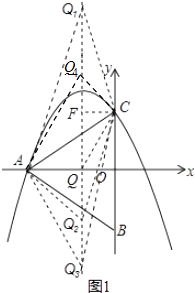
解：在抛物线的对称轴上存在点Q，使得△ACQ为等腰三角形，

当AQ=QC，如图1，

由（1）得：y=﹣ x2﹣ x+ =﹣ （x+1）2+ ，

即抛物线对称轴为：直线x=﹣1，则QO=1，AQ=2，

∵CO= ，QO=1，

∴QC=2，

∴AQ=QC，

∴Q（﹣1，0）；

当AC=Q1C时，过点C作CF⊥直线x=﹣1，于一点F，

则FC=1，

∵AO=3，CO= ，

∴AC=2 ，

∴Q1C=2 ，

∴FQ1= ，故Q1的坐标为：（﹣1， + ）；

当AC=CQ2=2 时，由Q1的坐标可得；Q2（﹣1，﹣ + ）；

当AQ3=AC=2 时，则QQ3 =2 ，故Q3（﹣1，﹣2 ），根据对称性可知Q4（﹣1，2 ）（Q4和Q3关于x轴对称）也符合题意，

综上所述：符合题意的Q点的坐标为：（﹣1，0）；（﹣1， + ）；（﹣1，﹣ + ）；（﹣1，﹣2 ），（﹣1，2 ）

（3）

解：如图2所示，

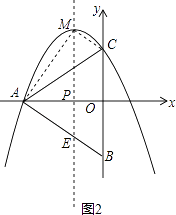
当四边形MEBC是平行四边形，则ME=BC，

∵AB=AC，且点A的坐标为（﹣3，0），点C坐标为（0， ），

∴B（0，﹣ ），

则BC=2 ，

设直线AB的解析式为：y=kx+e，

故 ，

解得： ，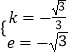

故直线AB的解析式为：y=﹣ x﹣ ，

设E（x，﹣ x﹣ ），M（x，﹣ x2﹣ x+ ），

故ME=﹣ x2﹣ x+ + x+ =﹣ x2﹣ x+2 =2 ，

解得：x1=0（不合题意舍去），x2=﹣1，

故P点在（﹣1，0），此时四边形MEBC是平行四边形；

四边形AECM是梯形，

理由：∵四边形MEBC是平行四边形，

∴MC∥AB，

∵CO= ，AO=3，

∴∠CAO=30°，

∵AC=AB，AO⊥BC，

∴∠BAO=30°，

∴∠BAC=60°，

∴△ABC是等边三角形，

∵AC=BC，ME=BC，所以AC=ME，

∴四边形AECM是等腰梯形．

【解析】（1）直接利用待定系数法求出抛物线解析式得出即可；（2）利用当AQ=QC，以及当AC=Q1C时，当AC=CQ2=2 时，当AQ3=AC=2 时，分别得出符合题意的答案即可；（3）利用平行四边形的性质首先得出BC的长，进而表示出线段ME的长，进而求出答案，再利用梯形的判定得出答案．
【考点精析】通过灵活运用二次函数的性质，掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小即可以解答此题．