Question

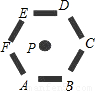
如图，有六个矩形水池环绕，矩形的内侧边所在直线恰好围成正六边形ABCDEF，正六边形的边长为4米．要从水源点P处向各水池铺设供水管道，这些管道的总长度最短是______米．（结果保留根号）

Answer 1

过点P作PG⊥ED于G，由于正六边形的中心角为360°÷6=60°．
所以∠P=30°，正六边形的边长为4米，则GD=

1

2

×4=2米．
PG=

GD

tan30°

=

2

3 3

=2

3

米．
根据垂线段最短，P到ED的最短距离为PG=2

3

米．
∴这些管道的总长度最短是6×2

3

=12

3

米．