题目内容
(2010•菏泽)如图所示,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,CD=5cm,求AB的长.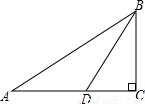
【答案】分析:先有∠A=30°,那么∠ABC=60°,结合BD是角平分线,那么可求出∠DBC=∠ABD=30°,在Rt△DBC中,利用直角三角形中30°的角所对的直角边等于斜边的一半,可求出BD,再利用勾股定理可求BC,同理,在Rt△ABC中,AB=2BC,即可求AB.
解答:解:∵在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,
∴∠ABD=∠CBD=30°,
∴AD=DB,
又∵Rt△CBD中,CD=5cm,
∴BD=10cm,
∴BC= =
= =5
=5 cm,
cm,
∴AB=2BC=10 cm.
cm.
点评:本题利用了角平分线定义、直角三角形中30°的角所对的直角边等于斜边的一半、勾股定理等知识.
解答:解:∵在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,
∴∠ABD=∠CBD=30°,
∴AD=DB,
又∵Rt△CBD中,CD=5cm,
∴BD=10cm,
∴BC=
 =
= =5
=5 cm,
cm,∴AB=2BC=10
 cm.
cm.点评:本题利用了角平分线定义、直角三角形中30°的角所对的直角边等于斜边的一半、勾股定理等知识.

练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
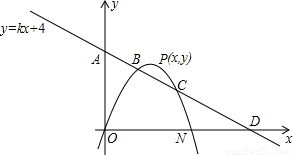
 ?若存在,请求出点P的坐标;若不存在,请说明理由.
?若存在,请求出点P的坐标;若不存在,请说明理由.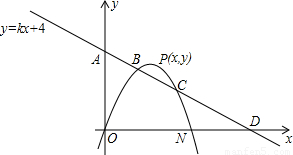
 ?若存在,请求出点P的坐标;若不存在,请说明理由.
?若存在,请求出点P的坐标;若不存在,请说明理由.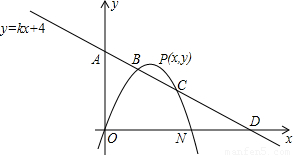
 ?若存在,请求出点P的坐标;若不存在,请说明理由.
?若存在,请求出点P的坐标;若不存在,请说明理由.