题目内容
(1)4(x-1)2=8
(2)若 +|n+2|=0,试求mn的立方根.
+|n+2|=0,试求mn的立方根.
解:(1)系数化为1得,(x-1)2=2,
∴x-1=± ,即x=1
,即x=1 ;
;
(2)∵ +|n+2|=0,
+|n+2|=0,
∴m-4=0,n+2=0,
∴m=4,n=-2,
∴mn=4×(-2)=-8,
∴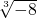 =-2,
=-2,
∴mn的立方根为-2.
分析:(1)先化为(x-1)2=2,再按直接开平方的方法解答即可;
(2)由非负数的性质,求出m,n的值,然后求mn的立方根即可.
点评:本题考查了一元二次方程的解法-直接开平方法、非负数的性质以及立方根的求法.
∴x-1=±
 ,即x=1
,即x=1 ;
;(2)∵
 +|n+2|=0,
+|n+2|=0,∴m-4=0,n+2=0,
∴m=4,n=-2,
∴mn=4×(-2)=-8,
∴
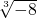 =-2,
=-2,∴mn的立方根为-2.
分析:(1)先化为(x-1)2=2,再按直接开平方的方法解答即可;
(2)由非负数的性质,求出m,n的值,然后求mn的立方根即可.
点评:本题考查了一元二次方程的解法-直接开平方法、非负数的性质以及立方根的求法.

练习册系列答案
相关题目
 甲、乙两组同学进行一分钟引体向上测试,评分标准规定,做6个以上(含6个)为合格,做9个以上(含9个)为优秀,两组同学的测试成绩如下表:
甲、乙两组同学进行一分钟引体向上测试,评分标准规定,做6个以上(含6个)为合格,做9个以上(含9个)为优秀,两组同学的测试成绩如下表:
| 成绩(个) | 4 | 5 | 6 | 7 | 8 | 9 |
| 甲组(人) | 1 | 2 | 5 | 2 | 1 | 4 |
| 乙组(人) | 1 | 1 | 4 | 5 | 2 | 2 |
(2)小斌对两组同学的测试成绩进行了如下的统计分析,请将下表补充完整:
| 统计量 | 平均数(个) | 中位数 | 众数 | 方差 | 合格率 | 优秀率 |
| 甲组 | 6.8 | 6 | 2.56 | 26.7% | ||
| 乙组 | 6.8 | 7 | 1.76 | 86.7% | 13.3% |

 ;
; ;
; 的整数有________.
的整数有________. 的同种零件,他们一天生产零件y(个)与生产时间t(时)的函数关系如图所示.
的同种零件,他们一天生产零件y(个)与生产时间t(时)的函数关系如图所示.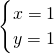 ,则这个方程组为 ________.
,则这个方程组为 ________.